
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Квадратичное отклонение | Квадратичное отклонение (далее К)квадратичное уклонение, стандартное отклонение величин x1, x2,..., xn от а - квадратный корень из выражения
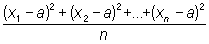 . .
Наименьшее значение Квадратичное отклонение имеет при а = 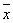 , где , где 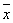 - среднее арифметическое величин x1, x2,..., xn: - среднее арифметическое величин x1, x2,..., xn:
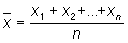 . .
В этом случае Квадратичное отклонение может служить мерой рассеяния системы величин x1, x2,..., xn. Употребляют также более общее понятие взвешенного Квадратичное отклонение
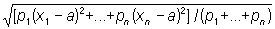 ; ;
числа p1,..., pn называют при этом весами, соответствующими величинам x1,..., xn. Взвешенное Квадратичное отклонение достигает наименьшего значения при а, равном взвешенному среднему:
(p1x1 +... + pnxn)/(p1 +...+ pn).
В теории вероятностей Квадратичное отклонение ох случайной величины Х (от ее математического ожидания) называют квадратный корень из дисперсии 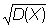 . .
Квадратичное отклонение употребляют как меру качества статистических оценок и называют в этом случае квадратичной ошибкой. См. Ошибок теория. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:18:31
|

|

|
 |
|

|
 |
 |
 |
|