
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Информации теория | Информации теория (далее И) математическая дисциплина, исследующая процессы хранения, преобразования и передачи информации. И - существенная часть кибернетики. В основе И лежит определенный способ измерения количества информации, содержащейся в каких-либо данных ("сообщениях"). И исходит из представления о том, что сообщения, предназначенные для сохранения в запоминающем устройстве или для передачи по каналу связи, не известны заранее с полной определенностью. Заранее известно лишь множество, из которого могут быть выбраны эти сообщения, и в лучшем случае - то, как часто выбирается то или иное из этих сообщений (т. е. вероятность сообщений). В И показывается, что "неопределенность", с которой сталкиваются в подобной обстановке, допускает количественное выражение и что именно это выражение (а не конкретная природа самих сообщений) определяет возможность их хранения и передачи. В качестве такой "меры неопределенности" в И принимается число двоичных знаков, необходимое для фиксирования (записи) произвольного сообщения данного источника. Более точно - рассматриваются все возможные способы обозначения сообщений цепочками символов 0 и 1 (двоичные коды), удовлетворяющие условиям: а) различным сообщениям соответствуют различные цепочки и б) по записи некоторой последовательности сообщений в кодированной форме эта последовательность должна однозначно восстанавливаться. Тогда в качестве меры неопределенности принимают среднее значение длины кодовой цепочки, соответствующее самому экономному способу кодирования; один двоичный знак служит единицей измерения (см. Двоичные единицы).
Пример. Пусть некоторые сообщения x1, x2, x3 появляются с вероятностями, равными соответственно 1/2, 3/8, 1/8. Какой-либо слишком короткий код, скажем
x1 = 0, x2 = 1, x3 = 01,
непригоден, так как нарушается вышеупомянутое условие б). Так, цепочка 01 может означать x1, x2 или x3. Код
x1 = 0, x2 = 10, x3 = 11,
удовлетворяет условиям а) и б). Ему соответствует среднее значение длины кодовой цепочки, равное
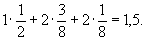
Нетрудно понять, что никакой другой код не может дать меньшего значения, т. е. указанный код - самый экономный. В соответствии с выбором меры неопределенности, неопределенность данного источника сообщении следует принять равной 1,5 двоичной единицы.
Здесь уместно подчеркнуть, что термины "сообщение", "канал связи" и т. п. понимают в И очень широко. Так, с точки зрения И, источник сообщений описывается перечислением множества x1, x2,... возможных сообщений (которые могут быть словами какого-либо языка, результатами измерений, телевизионными изображениями и т. п.) и соответствующих им вероятностей p1, p2,...
Нет никакой простой формулы, выражающей точный минимум ` среднего числа двоичных знаков, необходимого для кодирования сообщении x1, x2,..., xn через вероятности p1, p2,..., pn этих сообщений. Однако указанный минимум не меньше величины
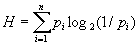
(где log2a обозначает логарифм числа a при основании 2) и может превосходить ее не более чем на единицу. Величина Н (энтропия множества сообщений) обладает простыми формальными свойствами, а для всех выходов И, которые носят асимптотический характер, соответствуя случаю ` R ¥, разница между и ` абсолютно несущественна. Поэтому именно энтропия принимается в качестве меры неопределенности сообщений данного источника. В приведенном выше примере энтропия равна
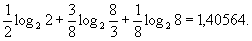
С изложенной точки зрения, энтропия бесконечной совокупности оказывается, как правило, бесконечной. Поэтому в применении к бесконечным совокупностям поступают иначе. Именно, задаются определенным уровнем точности и вводят понятие e - энтропии, как энтропии сообщения, записываемого с точностью до e, если сообщение представляет собой непрерывную величину или функцию (например, времени); подробнее см. в ст. Энтропия.
Так же как и понятие энтропии, понятие количества информации, содержащейся в одном случайном объекте (случайной величине, случайном векторе, случайной функции и т. д.) относительно другого, вводится сначала для объектов с конечным числом возможных значений. Затем общий случай изучается при помощи предельного перехода. В отличие от энтропии, количество информации, например, в одной непрерывно распределенной случайной величине относительно другой непрерывно распределенной величины очень часто оказывается конечным.
Понятие канала связи (см. Канал) в И носит весьма общий характер. По сути дела, канал связи задается указанием множества "допустимых сообщений" на "входе канала", множеством "сообщений на выходе" и набором условных вероятностей получения того или иного сообщения на выходе при данном входном сообщении. Эти условные вероятности описывают влияние "помех", искажающих передаваемые сообщения, "Присоединяя" к каналу какой-либо источник сообщений, можно рассчитать количество информации относительно сообщения на входе, содержащееся в сообщении на выходе. Верхняя грань таких количеств информации, взятая по всем допустимым источникам, называется пропускной способностью (емкостью) канала. Емкость канала - его основная информационная характеристика несмотря на влияние (возможно сильное) помех в канале, при определенном соотношении между энтропией поступающих сообщений и пропускной способностью канала возможна почти безошибочная передача (при надлежащем кодировании, см. Шеннона теорема).
И отыскивает оптимальные, в смысле скорости и надежности, способы передачи информации, устанавливая теоретические пределы достижимого качества. Как видно из предыдущего, И носит существенно статистический характер, и поэтому значительная часть ее математических методов заимствуется из теории вероятностей.
Основы И были заложены в 1948-49 американским ученым К. Шенноном. В ее теоретические разделы внесен вклад советским учеными А. Н. Колмогоровым и А. Я. Хинчиным, а в разделы, соприкасающиеся с применениями, - В. А. Котельниковым, А. А. Харкевичем и др.
Лит.: Яглом А. М., Яглом И. М., Вероятность и информация, 2 изд., М., 1960; Шэннон К., Статистическая теория передачи электрических сигналов, в кн.: Теория передачи электрических сигналов при наличии помех. Сб. переводов, М., 1953; Голдман С., Теория информации, пер. с англ., М., 1957; Теория информации и ее приложения. Сб. переводов, М., 1959; Хинчин А. Я., Понятие энтропии в теории вероятностей, "Успехи математических наук", 1953, т. 8, в. 3; Колмогоров А. Н., Теория передачи информации, М., 1956, (АН СССР. Сессия по научным проблемам автоматизации производства. Пленарное заседание); Питерсон У. У., Коды, исправляющие ошибки, пер. с англ., М., 1964.
Ю. В. Прохоров. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:14:11
|

|

|
 |
|

|
 |
 |
 |
|