
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Изопериметрические задачи | Изопериметрические задачи (далее И)(от изо... и периметр), класс задач вариационного исчисления. Простейшие Изопериметрические задачи (нахождение треугольников и многоугольников заданного периметра, имеющих наибольшую площадь; нахождение замкнутой кривой заданной длины, ограничивающей максимальную площадь; определение замкнутой поверхности заданной площади, ограничивающей наибольший объем, и т. п.) были известны древнегреческим ученым (Архимед, Зенодор и др.). Общее изучение Изопериметрические задачи началось в 1697, когда Я. Бернулли опубликовал поставленную и частично решенную им Изопериметрические задачи: среди всех кривых данной длины найти кривую, для которой некоторая величина, зависящая от кривой, достигает минимума или максимума. Систематическое исследование Изопериметрические задачи было впервые проведено в 1732 Л. Эйлером. Пример Изопериметрические задачи: среди кривых данной длины l, проходящих через точки А и , найти кривую, для которой площадь криволинейной трапеции (заштрихована на рис.) была бы наибольшей. Площадь криволинейной трапеции равна
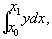 (1) (1)
длина дуги
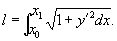 (2) (2)
Следовательно, задача сводится к нахождению наибольшего значения интеграла (1) при наличии условий (2). Оказывается, что искомая кривая - дуга окружности.
Лит.: Лаврентьев М. А., Люстерник Л. А., Курс вариационного исчисления, 2 изд., М. - Л., 1950.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 19.11.2024 20:30:08
|

|

|
 |
|

|
 |
 |
 |
|