|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Гаусса формулы | Гаусса формулы (далее Г), формулы, относящиеся к различным разделам математики и носящие имя К. Гаусса.
1) Квадратурные Г — формулы вида
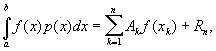
в которых узлы xk и коэффициенты Ak не зависят от функции f (x) и выбраны так, что формула точна (т. е. Rn = 0) для произвольного многочлена степени 2n - 1. В отличие от квадратурных формул Ньютона — Котеса, узлы в квадратурных Г, вообще говоря, не являются равноотстоящими. Если р (х) ³ 0 и
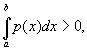
то для любого натурального n имеется единственная квадратурная Г Эти формулы имеют большое практическое значение, т.к. в ряде случаев они дают значительно большую точность, чем квадратурные формулы с тем же числом равноотстоящих узлов. Сам Гаусс исследовал (1816) случай р (х) º 1.
2) Г, выражающая полную кривизну К поверхности через коэффициенты ее линейного элемента; в координатах, для которых ds2 = l(du2 + dv2), Г имеет вид
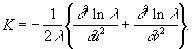
Эта формула была опубликована в 1827 и показывает, что полная кривизна не меняется при изгибании поверхности. Она составляет содержание одного из основных предложений созданной Гауссом внутренней геометрии поверхности.
3) Г для сумм Гаусса:
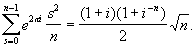
Эта формула была использована Гауссом (1801) в одном из доказательств закона взаимности квадратичных вычетов
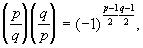
где р и q — нечетные простые числа, а 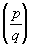 — Лежандра символ. Она явилась первым примером применения метода тригонометрических сумм в теории чисел. Этот метод был развит далее в работах Г. Вейля и особенно И. М. Виноградова и представляет собой один из наиболее мощных методов аналитической теории чисел.
4) Г для суммы гипергеометрического ряда. Если (c - b - a) > 0, то
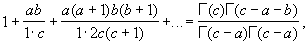
где Г (х) — гамма-функция. Опубликована в 1812.
С. Б. Стечкин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 11:58:30
|
|
|
|
|
|
|
|
|
|
|
