
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Сопряженные функции | Сопряженные функции (далее С) функции u (х, у), u(x, у) двух переменных х и у, связанные в некоторой области D условиями Коши — Римана (см. Коши—Римана уравнения);
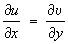 ; ; 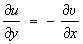 . .
При определенных условиях, например при непрерывности частных производных первого порядка, С u и u являются соответственно действительной и мнимой частью некоторой аналитической функции f (x + iy). Они удовлетворяют в области D уравнению Лапласа
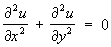 , , 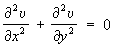
т. е. являются гармоническими функциями. Заданием функции, гармонической в односвязной области D (напр., u (х, у)) однозначно (с точностью до постоянного слагаемого) определяется сопряженная с ней гармоническая функция u(x, у), а тем самым и аналитическая функция f (x + iy). Например, если
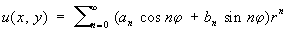
(j = arg (х + iy))
— гармоническая функция в некотором круге 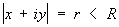 , то С , то С
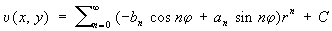
и
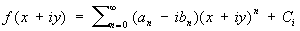
Значения С на круге r = 1 являются периодическими функциями аргумента j. Они раскладываются в тригонометрические ряды вида
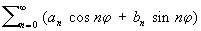
называемые сопряженными тригонометрическими рядами.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:28:22
|

|

|
 |
|

|
 |
 |
 |
|