
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Соприкасающаяся окружность | Соприкасающаяся окружность (далее С) в точке М кривой l, окружность, имеющая с / в точке М касание порядка n ³ 2 (см. Соприкосновение). Если кривизна кривой l в точке М равна нулю, то С вырождается в прямую. Т. к. порядок касания / и С в точке М не ниже двух, то С воспроизводит ход кривой вблизи точки касания с точностью до малых 3-го порядка по сравнению с размерами участка кривой. На рисунке изображено обычное (порядок касания кривой и С равен двум) взаимное расположение кривой и ее С: кривая пронизывает С в точке соприкосновения. Радиус С называют радиусом кривизны кривой / в точке М, а центр С — центром кривизны. Если кривая l плоская и задана уравнением у = f (x), то радиус С определяется формулой:
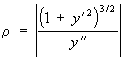 . .
Если кривая l — пространственная и задана уравнениями х = х (u), у = у (u), z = z (u), то радиус С определяется формулой:
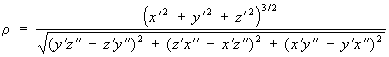
(здесь штрихи означают дифференцирование по параметру u).
Иногда С называют соприкасающимся кругом. См. также Дифференциальная геометрия.
Лит.: Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:21:55
|

|

|
 |
|

|
 |
 |
 |
|