
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Соответствия принцип | Соответствия принцип (далее С) постулат квантовой механики, требующий совпадений ее физических следствий в предельном случае больших квантовых чисел с результатами классической теории. В С проявляется тот факт, что квантовые эффекты существенны лишь при рассмотрении микрообъектов, когда величины размерности действия сравнимы с постоянной Планка 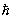 . Если же квантовые числа, характеризующие состояние физической системы (например, орбитальное квантовое число l), велики, то величиной . Если же квантовые числа, характеризующие состояние физической системы (например, орбитальное квантовое число l), велики, то величиной 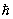 можно пренебречь и система с высокой точностью подчиняется классическим законам. С формальной точки зрения, С означает, что в пределе можно пренебречь и система с высокой точностью подчиняется классическим законам. С формальной точки зрения, С означает, что в пределе 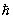 ® 0 квантово механическое описание физических объектов должно быть эквивалентно классическому. ® 0 квантово механическое описание физических объектов должно быть эквивалентно классическому.
Часто под С понимают следующее более общее положение. Любая новая теория, претендующая на более глубокое описание физической реальности и на более широкую область применимости, чем старая, должна включать последнюю как предельный случай. Так, релятивистская механика (см. Относительности теория) в пределе малых скоростей (v << c, где с — скорость света в вакууме) переходит в классическую. Формально переход осуществляется при с ® ¥.
Когда основные аксиомы теории уже сформулированы, С представляет в основном иллюстративный интерес, подчеркивая преемственность теоретических построений. В ряде случаев С помогает развить приближеные методы решения задач. Например, если в данной конкретной физической проблеме 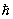 можно считать малой величиной, то это равносильно т. н. квазиклассическому приближению в квантовой механике. При этом нерелятивистское волновое Шредингера уравнение в пределе можно считать малой величиной, то это равносильно т. н. квазиклассическому приближению в квантовой механике. При этом нерелятивистское волновое Шредингера уравнение в пределе 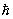 ® 0 приводит к классическому уравнению Гамильтона — Якоби. Однако в период возникновения новой теоретической дисциплины, когда ее принципы во многом еще не ясны, С имеет самостоятельное эвристическое значение. ® 0 приводит к классическому уравнению Гамильтона — Якоби. Однако в период возникновения новой теоретической дисциплины, когда ее принципы во многом еще не ясны, С имеет самостоятельное эвристическое значение.
С был выдвинут . Бором в 1923 (в т. н. старой квантовой теории, предшествующей квантовой механике) в связи с проблемой спектров излучения и поглощения Впоследствии, когда была создана последовательная квантовая механика, особенности спектров были объяснены на более глубокой основе, причем существенные черты математического аппарата определялись С
Значение С, однако, далеко выходит за рамки квантовой механики. Им широко пользуются в квантовой электродинамике, теории элементарных частиц и, без сомнения, он войдет составной частью в любую новую теоретическую схему.
Лит.: Бор Н., Три статьи о спектрах и строении пер. с нем.. М. — П., 1923; Блохинцев Д. И., Основы квантовой механики, 3 изд., М., 1961; Шифф Л., Квантовая механика, пер. с англ., М., 1957.
О. И. Завьялов.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:59:29
|

|

|
 |
|

|
 |
 |
 |
|