|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Сообщение | Сообщение (далее С) в теории информации, всякий носитель информации. При этом теория информации интересуется лишь количественной стороной информации, содержащейся в С Понятие С в теории информации имеет существенно вероятностный характер: каждый источник информации (или источник С) задается перечислением возможных С и соответствующих им вероятностей. Пусть x1, х2,..., xn — возможные С, a p1, p2,..., pn — соответствующие вероятности. Тогда количество информации в С xi принимают равным 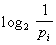 . Среднее количество информации в С данного источника (его энтропия), т. е. сумма
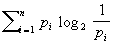
является важнейшей характеристикой источника. Именно величина энтропии определяет возможности передачи и хранения С, производимых источником.
Пример. Пусть источником С являются результаты последовательных измерений с точностью до 0,1 некоторой физической величины, равномерно распределенной в интервале от нуля до единицы. Тогда, если указывать только число десятых (с недостатком), возможными результатами отдельного измерения будут числа 0,1....,9. Вероятность появления каждого из них равна 0,1. С в данном примере представляются -членными последовательностями цифр. Вероятность каждого С равна (0,1) . Количество информации в каждом С и энтропия источника равны log2 10 = 3,32 двоичных единиц. Можно сказать, что источником С в этом примере является случайная последовательность десятичных знаков (цифр) длины . Именно такую форму случайных последовательностей знаков (или более общим образом — форму случайных процессов) имеют источники С. рассматриваемые в теории информации.
При изучении конкретных типов С, таких, как письменная речь, телеграфные, телефонные или телевизионные сигналы, обычно строится та или иная приближенная вероятностная модель источника С Так, с достаточной для целей теории информации точностью в качестве модели русской письменной речи может быть принята т. н. сложная цепь Маркова. Для непрерывных С в качестве моделей используются стационарные случайные процессы. Построение подобных моделей опирается на обширные статистические данные, касающиеся рассматриваемых процессов.
Ю. В. Прохоров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 11:30:02
|
|
|
|
|
|
|
|
|
|
|
