|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Больцмана статистика | Больцмана статистика (далее Б) физическая статистика для систем из большого числа невзаимодействующих частиц. Строго Б подчиняются и молекулярные идеальные газы, т. е. газы, у которых потенциальная энергия взаимодействия молекул считается равной нулю. Реально к таким системам относятся разреженные газы, молекулы которых слабо взаимодействуют друг с другом.
При большом числе частиц в системе невозможно детально описать поведение каждой частицы. Однако общие черты поведения системы в целом являются усредненным отражением движения отдельных частиц. Частицы распределяются по возможным для них состояниям — их координаты r и импульсы р принимают определенные значения. Математически это описывается функцией распределения, характеризующей вероятность пребывания частицы в данном состоянии.
Для идеального газа молекул, находящихся в поле внешних сил, функция распределения Больцмана имеет вид:
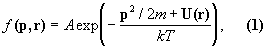
где р2/2m — кинетическая энергия молекулы массы m, (r) — ее потенциальная энергия во внешнем поле, k — Больцмана постоянная, Т — абсолютная температура газа; постоянная А определяется из условия, что суммарное число частиц, распределенных по всем возможным состояниям, равно полному числу частиц в системе (условие нормировки). Так как величина kT характеризует среднюю энергию теплового движения молекулы, то в Б распределение частиц по состояниям определяется отношением полной энергии частицы (кинетическая плюс потенциальная) к энергии ее теплового движения.
Функция распределения (1) содержит два сомножителя: ехр (-р2/2mкТ) и exp (- (r)/kT). Первый из них определяет распределение молекул по импульсам (или скоростям), т. е. является Максвелла распределением, а второй — распределение по координатам в поле внешних сил. Поэтому иногда только вторую зависимость называют распределением Больцмана, а формулу (1) называют распределением Максвелла — Больцмана.
С помощью функции распределения Больцмана легко получить формулу изменения концентрации молекул воздуха (независимо от их импульса) с изменением высоты над земной поверхностью, а следовательно, и барометрическую формулу, определяющую зависимость давления воздуха от высоты.
В квантовой статистике вместо функции распределения рассматривается среднее число частиц 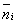 , находящихся в данном квантовом состоянии с энергией Ei, и распределение Больцмана выглядит следующим образом:
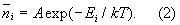
Постоянная А находится из условия
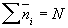
где — общее число частиц в системе, и равна А = (/)(h2/mkT)3/2 ( — объем газа, h — Планка постоянная). Распределение (2) является предельным случаем квантовых статистик Бозе — Эйнштейна и — Дирака, когда можно пренебречь квантовомеханическими эффектами, связанными с взаимным влиянием тождественных частиц (см. Тождественности принцип). Оно справедливо для систем, у которых все числа 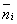 малы по сравнению с 1; это означает, что частицы проводят почти все время в сильно различающихся состояниях и потому специфическое влияние их друг на друга не проявляется.
Квантовая Б справедлива при малых плотностях газа / и высоких температурах (при данной массе частиц). Фактически Б применима для всех разреженных молекулярных газов, т.к. масса молекул велика и квантовое воздействие тождественных частиц друг на друга должно было бы проявиться лишь при столь высоких плотностях и низких температурах, которые соответствуют твердому (для — жидкому) состоянию вещества (а в этом случае Б вообще неприменима, т.к. взаимодействие молекул велико). К электронному газу в металлах и газу световых квантов — фотонов — Б неприменима (см. Статистическая физика).
Лит. см. при ст. Статистическая физика.
В. П. Павлов. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.02.2025 02:18:18
|
|
|
|
|
|
|
|
|
|
|
