
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Метрическое пространство | Метрическое пространство (далее М)множество объектов (точек), на котором введена метрика. Всякое Метрическое пространство является топологическим пространством; за окрестности в нем принимаются всевозможные открытые шары (при этом открытым шаром радиуса R с центром в точке x0 называется совокупность всех точек х, для которых расстояние r(х, x0) < R). Топология одного и того же множества может быть различной в зависимости от метрики, введенной на нем. Например, на множестве вещественных функций, определенных и непрерывных на отрезке (a, b) числовой оси, можно ввести две метрики:
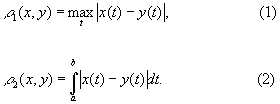
Соответствующие Метрическое пространство обладают разными топологическими свойствами. Метрическое пространство с метрикой (1) является полным (для любой последовательности его точек {xn} такой, что r1(xn, xm) ® 0 При n, m ® ¥, найдется элемент x0 Метрическое пространство, являющийся пределом этой последовательности); Метрическое пространство с метрикой (2) этим свойством не обладает. В Метрическое пространство можно вводить фундаментальные понятия анализа: непрерывность отображения одного Метрическое пространство в другое, сходимость, компактность и т.д. Понятие "Метрическое пространство" было введено М. Фреше в 1906.
Лит.: Александров П. С., Введение в общую теорию множеств и функций, М. — Л. 1948; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965.
В. И. Соболев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 01:39:16
|

|

|
 |
|

|
 |
 |
 |
|