
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Метрика (матем. термин) | Метрика (далее М) математический термин, обозначающий правило определения того или иного расстояния между любыми двумя точками (элементами) данного множества А. При этом расстоянием r(а, b) между точками а и b множества А называется вещественная числовая функция, удовлетворяющая следующим условиям:
1) r(а, b) ³ 0, причем r(а, b) = 0 тогда и только тогда, когда а = b,
2) r(а, b) = r(b, а); 3) r(а, b) + r(b, с) ³ r(а, с). На одном и том же множестве М (матем. термин) может вводиться различным образом. Например, на плоскости за расстояние между точками а и b, имеющими координаты (x1, y1) и (х2, y2) соответственно, можно принять не только обычное евклидово расстояние
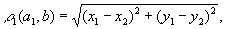
но и различные другие расстояния, например
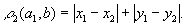
В векторных пространствах (функциональных и координатных) М (матем. термин) часто задаются нормы, иногда - с помощью скалярного произведения. В дифференциальной геометрии М (матем. термин) вводится путем задания элемента длины дуги при помощи дифференциальной квадратичной формы (см. Римановы геометрии). Множество с введенной на нем М (матем. термин) называется метрическим пространством.
Иногда под М (матем. термин) понимают правило определения не только расстояний, но и углов; например, проективная метрика.
В. И. Соболев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 01:33:41
|

|

|
 |
|

|
 |
 |
 |
|