
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Менье теорема | Менье теорема (далее М) теорема дифференциальной геометрии, устанавливающая свойство кривизн плоских сечений поверхности (см. Кривизна). Пусть p — произвольная плоскость, проведенная через касательную МТ в точке М к поверхности , q — ее угол с нормалью MN к поверхности, 1/R — кривизна в точке М кривой DMC, по которой поверхность пересекается плоскостью s, проходящей через нормаль MN и прямую МТ (DMC — т. н. нормальное сечение поверхности). Тогда кривизна 1/r в точке М кривой AMB, по которой поверхность пересекается плоскостью s, связана с кривизной 1/R нормального сечения соотношением
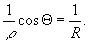
Эта формула и выражает теорему Менье. М была установлена Ж. Менье в 1776, но опубликована лишь в 1785.
Лит.: Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.03.2026 23:53:26
|

|

|
 |
|

|
 |
 |
 |
|