Маятник

Маятник (далее М), твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или оси. В физике под М обычно понимают М, совершающий колебания под действием силы тяжести; при этом его ось не должна проходить через центр тяжести тела. Простейший М состоит из небольшого массивного груза , подвешенного на нити (или легком стержне) длиной l. Если считать нить нерастяжимой и пренебречь размерами груза по сравнению с длиной нити, а массой нити по сравнению с массой груза, то груз на нити можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l от точки подвеса (рис. 1, а). Такой М называется математическим. Если же, как это обычно имеет место, колеблющееся тело нельзя рассматривать как материальную точку, то М называется физическим.   Математический маятник. Если М, отклоненный от равновесного положения 0, отпустить без начальной скорости или сообщить точке скорость, направленную перпендикулярно и лежащую в плоскости начального отклонения, то М будет совершать колебания в одной вертикальной плоскости по дуге окружности (плоский, или круговой математический М). В этом случае положение М определяется одной координатой, например углом j, на который М отклонен от положения равновесия. В общем случае колебания М не являются гармоническими; их период T зависит от амплитуды. Если же отклонения М малы, он совершает колебания, близкие к гармоническим, с периодом: 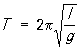   , где g — ускорение свободного падения; в этом случае период T не зависит от амплитуды, то есть колебания изохронны.   Если отклоненному М сообщить начальную скорость, не лежащую в плоскости начального отклонения, то точка будет описывать на сфере радиуса l кривые, заключенные между 2 параллелями z = z1 и z = z2 (рис. 2, а), где значения z1 и z2 зависят от начальных условий (сферический маятник). В частном случае, при z1 = z2 (рис. 2, б) точка будет описывать окружность в горизонтальной плоскости (конический маятник). Из некруговых М особый интерес представляет циклоидальный маятник, колебания которого изохронны при любой величине амплитуды.   Физический маятник. Физическим М обычно называется твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса (рис. 1, б). Движение такого М вполне аналогично движению кругового математического М При малых углах отклонения j М также совершает колебания, близкие к гармоническим, с периодом 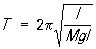   ,   где — момент инерции М относительно оси подвеса, l — расстояние от оси подвеса до центра тяжести , M — масса М Следовательно, период колебаний физического М совпадает с периодом колебаний такого математического М, который имеет длину l0 = /Ml. Эта длина называется приведенной длиной данного физического М   Точка на продолжении прямой , находящаяся на расстоянии l0 от оси подвеса, называется центром качаний физ. М При этом расстояние = l0 всегда больше, чем = l. Точка оси подвеса М и центр качаний обладают свойством взаимности: если ось подвеса сделать проходящей через центр качаний, то точка прежней оси подвеса станет новым центром качаний и период колебаний М не изменится. Это свойство взаимности используется в оборотном маятнике для определения приведенной длины l0; зная l0 и T, можно найти значение g в данном месте.   Свойствами М широко пользуются в различных приборах: в часах, в приборах для определения ускорения силы тяжести (см. Мовый прибор), ускорений движущихся тел, колебаний земной коры (см. Сейсмограф), в гироскопических устройствах, в приборах для экспериментального определения моментов инерции тел и других. См. также Фуко маятник.   Лит.: Бухгольц Н. Н., Основной курс теоретической механики, ч. 1, М, 1967, § 38, пп. 5, 13, 14; ч. 2, М, 1969, § 12, п. 4; Тарг С. М, Краткий курс теоретической механики, 7 изд., М, 1970, гл. 28, § 155; Хайкин С. Э., Физические основы механики, 2 изд., М, 1971, гл. 13, § 90, 91.   С. М Тарг.