
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Массового обслуживания теория | Массового обслуживания теория (далее М), математическая дисциплина, изучающая системы, предназначенные для обслуживания массового потока требований случайного характера (случайными могут быть как моменты появления требований, так и затраты времени на их обслуживание). Типичным примером объектов М могут служить автоматические телефонные станции, на которые случайным образом поступают "требования" — вызовы абонентов, а "обслуживание" состоит в соединении абонентов с другими абонентами, поддержании связи во время разговора и т. д. Целью развиваемых в М методов является, в конечном счете, отыскание разумной организации обслуживания, обеспечивающей заданное его качество. С этой точки зрения М рассматривают как часть операций исследования.
М широко использует аппарат теории вероятностей и (в меньшей степени) математической статистики. Задачи М, сформулированные математически, обычно сводятся к изучению специального типа случайных процессов. Исходя из заданных вероятностных характеристик поступающего потока вызовов и продолжительности обслуживания и учитывая схему системы обслуживания (наличие отказов или очередей и т. п., см. также Очередей теория), М определяет соответствующие характеристики качества обслуживания (вероятность отказа, среднее время ожидания начала обслуживания, среднее время простоя линий связи и т. д.). В ряде более простых случаев это определение возможно аналитическими методами, в более сложных случаях приходится прибегать к моделированию соответствующих случайных процессов по Монте-Карло методу.
Пример. Предположим, что автоматическая линия связи имеет n одинаково доступных для абонентов каналов. Вызовы поступают в случайные моменты времени. Если при поступлении очередного вызова все n каналов линии связи оказываются занятыми, то поступивший вызов получает отказ и теряется. В противном случае немедленно начинается разговор по одному из свободных каналов, длящийся, вообще говоря, случайное время.
Одной из характеристик эффективности работы такой линии связи является доля вызовов, получающих отказ, то есть предел р при Т®¥ (если он существует) отношения nT/T числа nT вызовов, потерянных в течение времени Т, к общему числу T вызовов, поступивших за это время. Этот предел можно назвать вероятностью отказа.
Другим, не менее естественным, показателем качества работы линии связи может служить относительное время ее занятости, то есть предел р* при T®¥ (если он существует) отношения tТ/Т, где tТ — суммарное время, в течение которого за период Т все n каналов линии связи одновременно заняты. Этот предел можно назвать вероятностью занятости. Обозначим X(t) число каналов, занятых в момент t. Тогда можно показать, что: 1) если моменты поступления вызовов образуют пуассоновский поток однородных событий, 2) длительности разговоров последовательных абонентов суть независимые (между собой и от моментов поступления вызовов) одинаково распределенные случайные величины, то случайный процесс X(t), t ³ 0, обладает эргодическим распределением, то есть существуют (не зависящие от начального распределения Х(0)) пределы
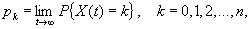
причем
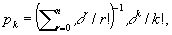 (*) (*)
где r — произведение интенсивности потока поступлений вызовов на среднюю длительность разговора отдельного абонента. Кроме того, в этом случае р = р*, и их общее значение равно pn. Формулы (*) используются для расчета минимального количества каналов линии связи, обеспечивающей заданную вероятность отказа. Эти формулы называются Эрланга формулами. Следует добавить, что при отказе от условия 1) равенство р = р* может не выполняться.
Становление М было вызвано интересом к математическим задачам, возникающим в организации телефонных сетей, датского инженера А. К. Эрланга, первые публикации которого относятся к 20-м годам 20 века. М получила дальнейшее развитие в 40—50-х годах в работах К. Пальма (Швеция), Ф. Поллачека ( А. Я. Хинчина (СССР). Последнему принадлежит сам термин "М". Эти работы были продолжены советским математиком Б. В. Гнеденко и другими. Развитие М в значительной мере стимулируется расширением круга ее применений. Являясь формально частью теории случайных процессов, М выделилась в самостоятельную область исследований со своим кругом задач и методов их решения и в свою очередь стимулирует развитие теории случайных процессов.
Лит.: Хинчин А. Я., Работы по математической теории массового обслуживания, М., 1963; Розенберг В. Я., Прохоров А. И., Что такое теория массового обслуживания, М., 1965; Гнеденко Б. В., Коваленко И. Н., Введение в теорию массового обслуживания, М., 1966; Саати Т. Л., Элементы теории массового обслуживания и ее приложения, перевод с английского, М., 1971; Боровков А. А., Вероятностные процессы в теории массового обслуживания, М., 1972.
О. В. Висков. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:31:48
|

|

|
 |
|

|
 |
 |
 |
|