
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Малые выборки | Малые выборки (далее М), статистические выборки столь малого объема n, что к ним нельзя применить простые классические формулы, действующие лишь асимптотически при n ® ¥. Особенности статистической оценки параметров по М легче всего понять на примере нормального распределения (для которого малыми обычно считают выборки объема n £ 30). Пусть необходимо оценить неизвестное среднее значение a выборки x1, x2, ..., xn из нормальной совокупности с неизвестной дисперсией s2. Обозначим
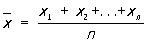 , ,
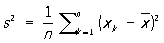 . .
Исходным пунктом при оценке a служит то обстоятельство, что распределение вероятностей величины
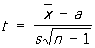
не зависит от а и s.
Вероятность w неравенства - tw < t < tw и равносильного ему неравенства
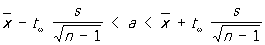 (1) (1)
вычисляется при этом по формуле
w = 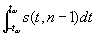 (2) (2)
где s(t, n - 1) есть плотность вероятности для так называемого Стьюдента распределения с n - 1 степенями свободы. Определяя для заданных n и w (0 < w < 1) соответствующее tw (что можно сделать, например, по таблицам), получают правило (1) нахождения доверительных границ для величины а, имеющей значимости уровень w.
При больших n формула (2), связывающая w и tw, приближенно может быть заменена формулой
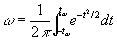 (3) (3)
Эту формулу иногда неправильно применяют для определения tw при небольших n, что приводит к грубым ошибкам. Так, для w = 0,99 по формуле (3) находим t0,99 = 2,58; истинные значения t0,99 для малых n приведены в следующей таблице:
n< | 2< | 3< | 4< | 5< | 10< | 20< | 30< |
t0,99
|
63,66
|
9,92
|
5,84
|
4,60
|
3,25
|
2,86
|
2,76
|
Если пользоваться формулой (3) при n = 5, то получится вывод, что неравенство
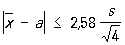
выполняется с вероятностью 0,99. В действительности в случае пяти наблюдений вероятность этого неравенства равна лишь 0,94, а вероятностью 0,99 обладает в соответствии с приведенной таблицей неравенство
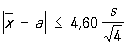
Об оценке по М теоретической дисперсии s2 см. "Хи-квадрат" распределение. Разработаны также аналогичные методы оценки по М параметров многомерных распределении (например, коэффициента корреляции).
Лит.: Крамер Г., Математические методы статистики, перевод с английского, М., 1948; Колмогоров А. Н., Определение центра рассеивания и меры точности по ограниченному числу наблюдений, "Известия АН СССР. Серия математическая", 1942, т. 6, № 1-2; Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, М., 1965.
Ю. В. Прохоров. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:58:21
|

|

|
 |
|

|
 |
 |
 |
|