|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Максимального правдоподобия метод | Максимального правдоподобия метод (далее М) метод нахождения статистических оценок неизвестных параметров распределения; согласно М, в качестве оценок выбираются те значения параметров, при которых данные результаты наблюдений "наиболее вероятны". Предполагается, что результаты наблюдений X1, ..., Xn являются взаимно независимыми случайными величинами с одним и тем же распределением вероятностей, зависящим от одного неизвестного параметра q Î Q, где Q — множество допустимых значений q. Для придания точного смысла принципу "наибольшей вероятности" поступают следующим образом. Вводят функцию
 ,
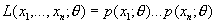где p(t; q) в случае непрерывного распределения интерпретируется как плотность вероятности случайной величины X, а в дискретном случае — как вероятность того, что случайная величина Х примет значение t. Функцию L(X1, . . ., Xn; q) от случайных величин X1, . . ., Xn называют функцией правдоподобия, а оценкой максимального правдоподобия параметра q называют такое значение 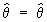 (X1, . . ., Xn) (само являющееся случайной величиной), при котором функция правдоподобия достигает наибольшего возможного значения. Так как точка максимума для log L та же, что и для L, то для нахождения оценок максимального правдоподобия следует решить так называемое уравнение правдоподобия
 .
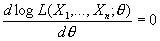М не всегда приводит к приемлемым результатам, однако в достаточно широком круге практически важных случаев этот метод является в известном смысле наилучшим. Так, например, можно утверждать, что если для параметра q существует несмещенная эффективная оценка q* по выборке объема n, то уравнение правдоподобия имеет единств, решение 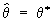 . Что касается асимптотического поведения оценок максимального правдоподобия при больших n, то известно, что при некоторых общих условиях М приводит к состоятельной оценке, которая асимптотически нормальна и асимптотически эффективна. Данные выше определения непосредственно обобщаются и на случай нескольких неизвестных параметров и на случай выборок из многомерных распределений. М в его современном виде был предложен английским статистиком Р. Фишером (1912), однако в частных формах метод использовался К. Гауссом, а еще раньше, в 18 веке, к его идее были близки И. Ламберт и Д. Бернулли. Следует добавить, что название "М" является калькой с английского "maximum likelihood method".
Лит.: Крамер Г., Математические методы статистики, перевод с английского, М., 1948; Рао С. Р., Линейные статистические методы и их применения, перевод с английского, М., 1968; Худсон Д., Статистика для физиков, перевод с английского, М., 1970.
А. В. Прохоров. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.12.2024 02:50:13
|
|
|
|
|
|
|
|
|
|
|
