
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Коши задача | Коши задача (далее К) одна из основных задач теории дифференциальных уравнений, впервые систематически изучавшаяся О. Коши. Заключается в нахождении решения u (x, t); х = (x1,..., xn) дифференциального уравнения вида:
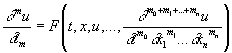 , (1) , (1)
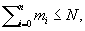 m0 < m, m > 0, m0 < m, m > 0,
удовлетворяющего т. н. начальным условиям.
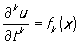 , t = t0, x Î G0, k = 0, …, m-1, (2) , t = t0, x Î G0, k = 0, …, m-1, (2)
где G0 — носитель начальных данных — область гиперплоскости t = to пространства переменных x1,..., xn. Когда и fk, k = 0,..., m — 1, являются аналитическими функциями своих аргументов, задача Коши (1), (2) в некоторой области G пространства переменных t, х, содержащей G0, всегда имеет и притом единственное решение. Однако это решение может оказаться неустойчивым (т. е. малое изменение начальных данных может вызвать сильное изменение решения), например в том случае, когда уравнение (1) принадлежит эллиптическому типу. При неаналитических данных задача Коши (1), (2) может потерять смысл, если не ограничиться рассмотрением того случая, когда уравнение (1) является гиперболическим.
Лит.: Курант Р., Гильберт Д., Методы математической физики, пер. с нем., т. 2, М.— Л., 1951; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.
А. В. Бицадзе. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 00:06:29
|

|

|
 |
|

|
 |
 |
 |
|