
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Корректные и некорректные задачи | Корректные и некорректные задачи (далее К) классы математических задач, которые различаются степенью определенности их решений. Многие математические задачи состоят в том, что по исходным данным u ищется решение z. При этом считается, что u и z связаны функциональной зависимостью z = R (u). Задача называется корректной задачей (или корректно поставленной), если выполнены следующие условия (условия корректности): 1) задача имеет решение при любых допустимых исходных данных (существование решения); 2) каждым исходным данным u соответствует только одно решение (однозначность задачи); 3) решение устойчиво.
Смысл первого условия заключается в том, что среди исходных данных нет противоречащих друг другу условий, что исключало бы возможность решения задачи.
Второе условие означает, что исходных данных достаточно для однозначной определенности решения задачи. Эти два условия обычно называют условиями математической определенности задачи.
Третье условие заключается в следующем. Если u1 и u2 - два различных набора исходных данных, мера уклонения которых друг от друга достаточно мала, то мера уклонения решений z1 = R (u1) и z2 = R (u2) меньше любой наперед заданной меры точности. При этом предполагается, что в многообразии = {u} допустимых исходных данных и в многообразии возможных решений Z = {z} установлено понятие меры уклонения (или меры близости) r(u1, u2) и r*(z1, z2). Третье условие обычно трактуется как физическая детерминированность задачи. Это объясняется тем, что исходные данные физической задачи, как правило, задаются с некоторой погрешностью; при нарушении же третьего условия как угодно малые возмущения исходных данных могут вызывать большие отклонения в решении.
Задачи, не удовлетворяющие хотя бы одному условию корректности, называются некорректными задачами (или некорректно поставленными).
Внимание к корректности задач было привлечено французским математиком Ж. Адамаром в связи с решением краевых задач для уравнений с частными производными. Понятие корректности задач явилось, в частности, поводом для классификации краевых задач таких уравнений.
Существовало мнение, что некорректные задачи не могут встречаться при решении физических и технических задач и что для некорректных задач невозможно построение приближенного решения в случае отсутствия устойчивости. Расширение средств автоматизации при получении экспериментальных данных привело к большому увеличению объема таких данных; необходимость установления по ним информации о естественнонаучных объектах потребовала рассмотрения некорректных задач. Развитие электронной вычислительной техники и применение ее к решению математических задач изменило точку зрения на возможность построения приближенных решений некорректно поставленных задач.
Понятия приближенного решения для К. и н. з. существенно различны. В качестве приближенного решения z = R (u) корректной задачи можно брать точное ее решение 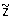 с приближенными исходными данными с приближенными исходными данными 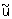 , т. к. для любой точности e приближенного решения корректной задачи в силу третьего условия существует такая точность d(e) исходных данных, что, если , т. к. для любой точности e приближенного решения корректной задачи в силу третьего условия существует такая точность d(e) исходных данных, что, если 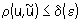 , то , то  . Для некорректных задач точное решение с приближенными исходными данными нельзя принимать в качестве приближенного решения. Однако задание приближенных исходных данных в естественных науках может быть охарактеризовано не только исходным элементом . Для некорректных задач точное решение с приближенными исходными данными нельзя принимать в качестве приближенного решения. Однако задание приближенных исходных данных в естественных науках может быть охарактеризовано не только исходным элементом 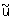 , но и мерой его точности d. Т. о., для определения приближенного решения имеется не только элемент , но и мерой его точности d. Т. о., для определения приближенного решения имеется не только элемент 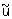 , но и параметр d. Понятие приближенного решения задачи z = R (u) вводится с помощью т. н. параметрического оператора Rd(u), зависящего от параметра d и называемого регуляризирующим (или исправляющим) оператором. Если оператор Rd(u) определен для всех d > 0 и всех , но и параметр d. Понятие приближенного решения задачи z = R (u) вводится с помощью т. н. параметрического оператора Rd(u), зависящего от параметра d и называемого регуляризирующим (или исправляющим) оператором. Если оператор Rd(u) определен для всех d > 0 и всех 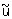 , входящих в класс допустимых исходных данных, и если z = R (u), то для любой заданной точности e существует (хотя бы в принципе) такое d(e), что для любого элемента , входящих в класс допустимых исходных данных, и если z = R (u), то для любой заданной точности e существует (хотя бы в принципе) такое d(e), что для любого элемента 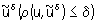 решение решение 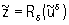 уклоняется от z меньше, чем на заданную точность e, т. е. уклоняется от z меньше, чем на заданную точность e, т. е. 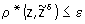 . .
Т. о., приближенное решение некорректной задачи может быть сведено к нахождению регуляризирующего оператора 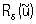 , который определяет устойчивое приближение к z. , который определяет устойчивое приближение к z.
Примером некорректной классической математической задачи может служить задача приближенного дифференцирования при определенных (практически важных) мерах точности задания z и u. Именно, некорректной будет задача о нахождении равномерного приближения 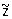 к z по равномерному приближению к z по равномерному приближению 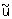 к u, т. к. здесь не выполнено первое условие корректности: не для всякой функции к u, т. к. здесь не выполнено первое условие корректности: не для всякой функции 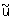 такой, что такой, что 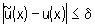 существует производная существует производная 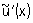 , а также не выполняется третье условие корректности: если даже существует производная , а также не выполняется третье условие корректности: если даже существует производная 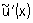 , то из неравенства , то из неравенства 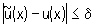 не следует близость производных не следует близость производных 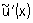 и u"(х). Однако в качестве регуляризирующего оператора можно взять и u"(х). Однако в качестве регуляризирующего оператора можно взять 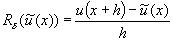 при h >> d. Этот оператор определен для всех при h >> d. Этот оператор определен для всех  независимо от их дифференцируемости и в ограниченном промежутке дает равномерное приближение для всякой непрерывно дифференцируемой функции u (х). независимо от их дифференцируемости и в ограниченном промежутке дает равномерное приближение для всякой непрерывно дифференцируемой функции u (х).
Можно привести много др. примеров классических математических задач, являющихся некорректными при совершенно естественном выборе понятий меры точности как для исходных данных задачи, так и для возможных решений: решение систем линейных алгебраических уравнений с определителем, равным нулю; задача оптимального планирования; решение интегральных уравнений 1-го рода; задача аналитического продолжения; суммирование рядов Фурье; большое число краевых задач для уравнении с частными производными.
Обширный класс некорректно поставленных задач в естествознании составляют задачи обработки наблюдений без дополнительной (количественной) информации о свойствах решений. Если изучается объект, количественные характеристики z которого недоступны для прямого изучения, то обычно исследуются некоторые проявления этого объекта u, функционально зависящие от z. Задача обработки наблюдений состоит в решении "обратной задачи", т. е. в определении характеристики z объекта по результатам наблюдений u; при этом u задается приближенно.
Имеется много работ (особенно советских математиков), посвященные методам приближенного решения некорректно поставленных задач и их применений к решению обратных задач. Эти работы имеют важное значение для автоматизации обработки наблюдений, для решения проблем управления и т. д.
Лит.: Тихонов Д. Н., Об устойчивости обратных задач, "Доклады АН СССР", 1943, т. 39, № 5; его же, О решении некорректно поставленных задач и методе регуляризации, там же, 1963, т. 151, № 3; Лаврентьев М. М., О некоторых некорректных задачах математической физики, Новосиб., 1962.
А. Н. Тихонов. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 00:15:57
|

|

|
 |
|

|
 |
 |
 |
|