
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Корень (в математике) | Корень (далее К)в математике, 1) К(в математике) степени n из числа а - число х (обозначаемое 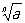 ), n-я степень которого равна а (то есть xn = а). Действие нахождения К(в математике) называют извлечением корня. При а ¹ 0 существует n различных значений К(в математике) (вообще говоря, комплексных); например, значениями ), n-я степень которого равна а (то есть xn = а). Действие нахождения К(в математике) называют извлечением корня. При а ¹ 0 существует n различных значений К(в математике) (вообще говоря, комплексных); например, значениями 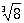 являются: 2; -1+i являются: 2; -1+i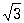 ; -1-i ; -1-i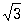 . К нахождению К(в математике) из чисел приводили различные геометрические задачи математиков глубокой древности. Среди вавилонских клинописных текстов (2-е тысячелетие до н. э.) имеются описания приближенного нахождения квадратного К(в математике) и таблицы квадратных К(в математике), а в египетских папирусах встречается для действия извлечения К(в математике) и особый знак. Древнегреческие математики установили несоизмеримость стороны квадрата с его диагональю (равной а . К нахождению К(в математике) из чисел приводили различные геометрические задачи математиков глубокой древности. Среди вавилонских клинописных текстов (2-е тысячелетие до н. э.) имеются описания приближенного нахождения квадратного К(в математике) и таблицы квадратных К(в математике), а в египетских папирусах встречается для действия извлечения К(в математике) и особый знак. Древнегреческие математики установили несоизмеримость стороны квадрата с его диагональю (равной а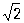 , если а - сторона), что позднее привело к открытию иррациональности. Ариабхата (5 в.) дал правила для извлечения квадратных и кубических К(в математике) Омар Хайям (2-я половина 11 - начало 12 вв.), аль-Каши (15 в.), немецкий математик М. Штифель (16 в.) извлекали К(в математике) высших степеней, исходя из формулы для (а+b) n. Л. Эйлер (18 в.) дал сохранившие свое значение до наших дней приближенные способы извлечения К(в математике) Квадратные К из отрицательных чисел, встречающиеся в 16 в. у Дж. Кардана и Р. Бомбелли, привели к открытию комплексных чисел. , если а - сторона), что позднее привело к открытию иррациональности. Ариабхата (5 в.) дал правила для извлечения квадратных и кубических К(в математике) Омар Хайям (2-я половина 11 - начало 12 вв.), аль-Каши (15 в.), немецкий математик М. Штифель (16 в.) извлекали К(в математике) высших степеней, исходя из формулы для (а+b) n. Л. Эйлер (18 в.) дал сохранившие свое значение до наших дней приближенные способы извлечения К(в математике) Квадратные К из отрицательных чисел, встречающиеся в 16 в. у Дж. Кардана и Р. Бомбелли, привели к открытию комплексных чисел.
2) К(в математике) алгебраического уравнения
a0xn + a1xn-1+... + an-1x + an = 0 (1)
- число с, которое после подстановки его вместо х обращает уравнение в тождество. К(в математике) уравнения (1) называется также и К(в математике) многочлена
f (x) = a0xn + a1xn-1+... + an-1x + an.
Если с является К(в математике) многочлена f (x), то f (x) делится без остатка на х-с. См. также Многочлен, Уравнение. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:48:22
|

|

|
 |
|

|
 |
 |
 |
|