
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Касательная плоскость | Касательная плоскость (далее К) к поверхности в точке М, плоскость, проходящая через точку М и характеризующаяся тем свойством, что расстояние от этой плоскости до переменной точки M" поверхности при стремлении M" к М является бесконечно малым по сравнению с расстоянием MM". Если поверхность задана уравнением z = f (x, у), то уравнение К в точке (x0, y0, z0), где z0 = f (x0, y0), имеет вид:
z — z0 = A (x — x0) + В (у — у0)
в том и только том случае, когда функция f (x, у) имеет в точке (x0, y0) полный дифференциал. В этом случае А и В суть значения частных производных 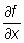 и и 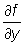 в точке (x0, y0) (см. Дифференциальное исчисление). в точке (x0, y0) (см. Дифференциальное исчисление). |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 00:09:35
|

|

|
 |
|

|
 |
 |
 |
|