
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Картографические проекции | Картографические проекции (далее К)отображения всей поверхности земного эллипсоида или какую-либо ее части на плоскость, получаемые в основном с целью построения карты.
Масштаб. Картографические проекции строятся в определенном масштабе. Уменьшая мысленно земной эллипсоид в М раз, например в 10 000 000 раз, получают его геометрическую модель — глобус, изображение которого уже в натуральную величину на плоскости дает карту поверхности этого эллипсоида. Величина 1: М (в примере 1: 10 000 000) определяет главный, или общий, масштаб карты. Т. к. поверхности эллипсоида и шара не могут быть развернуты на плоскость без разрывов и складок (они не принадлежат к классу развертывающихся поверхностей), любой Картографические проекции присущи искажения длин линий, углов и т.п., свойственные всякой карте. Основной характеристикой Картографические проекции в любой ее точке является частный масштаб m. Это — величина, обратная отношению бесконечно малого отрезка ds на земном эллипсоиде к его изображению ds на плоскости: 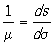 причем m зависит от положения точки на эллипсоиде и от направления выбранного отрезка. Ясно, что mmin £ m £ mmax, и равенство здесь возможно лишь в отдельных точках или вдоль некоторых линий на карте. Т. о., главный масштаб карты характеризует ее только в общих чертах, в некотором осредненном виде. Отношение m/М называют относительным масштабом, или увеличением длины, разность причем m зависит от положения точки на эллипсоиде и от направления выбранного отрезка. Ясно, что mmin £ m £ mmax, и равенство здесь возможно лишь в отдельных точках или вдоль некоторых линий на карте. Т. о., главный масштаб карты характеризует ее только в общих чертах, в некотором осредненном виде. Отношение m/М называют относительным масштабом, или увеличением длины, разность 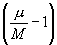 искажением длины. При анализе свойств Картографические проекции можно не принимать во внимание главный масштаб; численное значение его учитывается только при вычислениях координат точек Картографические проекции Поэтому часто, например в теории искажений, считают М = 1. искажением длины. При анализе свойств Картографические проекции можно не принимать во внимание главный масштаб; численное значение его учитывается только при вычислениях координат точек Картографические проекции Поэтому часто, например в теории искажений, считают М = 1.
Общие сведения. Теория Картографические проекции — математическая картография — имеет своей целью изучение всех видов искажений отображений поверхности земного эллипсоида на плоскость и разработку методов построения таких проекций, в которых искажения имели бы или наименьшие (в каком-либо смысле) значения или заранее заданное распределение.
Исходя из нужд картографии, в теории Картографические проекции рассматривают отображения поверхности земного эллипсоида на плоскость. Т. к. земной эллипсоид имеет малое сжатие, и его поверхность незначительно отступает от сферы, а также в связи с тем, что Картографические проекции необходимы для составления карт в средних и мелких масштабах (М > 1 000 000), то часто ограничиваются рассмотрением отображений на плоскость сферы некоторого радиуса R, отклонениями которой от эллипсоида можно пренебречь или каким-либо способом учесть. Поэтому далее имеются в виду отображения на плоскость хОу сферы, отнесенной к географическим координатам j (широта) и l (долгота).
Уравнения любой Картографические проекции имеют вид
x = f1(j, l), y = f2(j, l), (1)
где f1 и f2 — функции, удовлетворяющие некоторым общим условиям. Изображения меридианов l = const и параллелей j = const в данной Картографические проекции образуют картографическую сетку. Картографические проекции может быть определена также двумя уравнениями, в которых фигурируют не прямоугольные координаты х, у плоскости, а какие-либо иные. Некоторые Картографические проекции (например, перспективные проекции (в частности, ортографические, рис. 2) перспективно-цилиндрические (рис. 7) и др.) можно определить геометрическими построениями. Картографические проекции определяют также правилом построения соответствующей ей картографической сетки или такими ее характеристическими свойствами, из которых могут быть получены уравнения вида (1), полностью определяющие проекцию.
Краткие исторические сведения. Развитие теории Картографические проекции, как и всей картографии, тесно связано с развитием геодезии, астрономии, географии, математики. Научные основы картографии были заложены в Древней Греции (6—1 вв. до н. э.). Древнейшей Картографические проекции считается гномоническая проекция, примененная Фалесом Милетским к построению карт звездного неба. После установления в 3 в. до н. э. шарообразности Земли Картографические проекции стали изобретаться и использоваться при составлении географических карт (Гиппарх, Птолемей и др.). Значительный подъем картографии в 16 в., вызванный Великими географическими открытиями, привел к созданию ряда новых проекций; одна из них, предложенная Г. Меркатором, используется и в настоящее время (см. Меркатора проекция). В 17—18 вв., когда широкая организация топографических съемок стала поставлять достоверный материал для составления карт на значительной территории, Картографические проекции разрабатывались как основа для топографических карт (французский картограф Р. Бонн, Дж. Д. Кассини), а также выполнялись исследования отдельных наиболее важных групп Картографические проекции (И. Ламберт, Л. Эйлер, Ж. Лагранж и др.). Развитие военной картографии и дальнейшее увеличение объема топографических работ в 19 в. потребовали обеспечения математической основы крупномасштабных карт и введения системы прямоугольных координат на базе, более подходящей Картографические проекции Это привело К. Гаусса к разработке фундаментальной геодезической проекции. Наконец, в середине 19 в. А. Тиссо ( дал общую теорию искажений Картографические проекции Развитие теории Картографические проекции в России было тесно связано с запросами практики и дало много оригинальных результатов (Л. Эйлер, Ф. И. Шуберт, П. Л. Чебышев, Д. А. Граве и др.). В трудах советских картографов В. В. Каврайского, Н. А. Урмаева и др. разработаны новые группы К. и., отдельные их варианты (до стадии практического использования), важные вопросы общей теории Картографические проекции, классификации их и др.
Теория искажений. Искажения в бесконечно малой области около какой-либо точки проекции подчиняются некоторым общим законам. Во всякой точке карты в проекции, не являющейся равноугольной (см. ниже), существуют два таких взаимно перпендикулярных направления, которым на отображаемой поверхности соответствуют также взаимно перпендикулярные направления, это — так называемые главные направления отображения. Масштабы по этим направлениям (главные масштабы) имеют экстремальные значения: mmax= а и mmin= b. Если в какой-либо проекции меридианы и параллели на карте пересекаются под прямым углом, то их направления и есть главные для данной проекции. Искажение длины в данной точке проекции наглядно представляет эллипс искажений, подобный и подобно расположенный изображению бесконечно малой окружности, описанной вокруг соответствующей точки отображаемой поверхности. Полудиаметры этого эллипса численно равны частным масштабам в данной точке в соответствующих направлениях, полуоси эллипса равны экстремальным масштабам, а направления их — главные.
Связь между элементами эллипса искажений, искажениями Картографические проекции и частными производными функций (1) устанавливается основными формулами теории искажений.
Классификация картографических проекций по положению полюса используемых сферических координат. Полюсы сферы суть особые точки географической координации, хотя сфера в этих точках не имеет каких-либо особенностей. Значит, при картографировании областей, содержащих географические полюсы, желательно иногда применять не географические координаты, а другие, в которых полюсы оказываются обыкновенными точками координации. Поэтому на сфере используют сферические координаты, координатные линии которых, так называемые вертикалы (условная долгота на них а = const) и альмукантараты (где полярные расстояния z = const), аналогичны географическим меридианам и параллелям, но их полюс Z0 не совпадает с географическим полюсом 0 (рис. 1). Переход от географических координат j, l любой точки сферы к ее сферическим координатам z, a при заданном положении полюса Z0(j0, l0) осуществляется по формулам сферической тригонометрии. Всякая Картографические проекции, данная уравнениями (1), называется нормальной, или прямой (j0 = p/2). Если та же самая проекция сферы вычисляется по тем же формулам (1), в которых вместо j, l фигурируют z, a, то эта проекция называется поперечной при j0 = 0, l0 и косой, если 0 < j0 < p/2. Применение косых и поперечных проекций приводит к уменьшению искажений. На рис. 2 показана нормальная (а), поперечная (б) и косая (в) ортографические проекции сферы (поверхности шара).
Классификация картографических проекций по характеру искажений. В равноугольных (конформных) Картографические проекции масштаб зависит только от положения точки и не зависит от направления. Эллипсы искажений вырождаются в окружности. Примеры — проекция Меркатор, стереографическая проекция.
В равновеликих (эквивалентных) Картографические проекции сохраняются площади; точнее, площади фигур на картах, составленных в таких проекциях, пропорциональны площадям соответствующих фигур в натуре, причем коэффициент пропорциональности — величина, обратная квадрату главного масштаба карты. Эллипсы искажений всегда имеют одинаковую площадь, различаясь формой и ориентировкой.
Произвольные Картографические проекции не относятся ни к равноугольным, ни к равновеликим. Из них выделяют равнопромежуточные, в которых один из главных масштабов равен единице, и ортодромические, в которых большие круги шара (ортодромы) изображаются прямыми.
При изображении сферы на плоскости свойства равноугольности, равновеликости, равнопромежуточности и ортодромичности несовместимы. Для показа искажений в разных местах изображаемой области применяют: а) эллипсы искажений, построенные в разных местах сетки или эскиза карты (рис. 3); б) изоколы, т. е. линии равного значения искажений (на рис. 8в см. изоколы наибольшего искажения углов со и изоколы масштаба площадей р); в) изображения в некоторых местах карты некоторых сферических линий, обычно ортодромий (О) и локсодромий (Л), см. рис. 3а, 3б и др.
Классификация нормальных картографических проекций по виду изображений меридианов и параллелей, являющаяся результатом исторического развития теории Картографические проекции, объемлет большинство известных проекций. В ней сохранились наименования, связанные с геометрическим методом получения проекций, однако рассматриваемые их группы теперь определяют аналитически.
Цилиндрические проекции (рис. 3) — проекции, в которых меридианы изображаются равноотстоящими параллельными прямыми, а параллели — прямыми, перпендикулярными к изображениям меридианов. Выгодны для изображения территорий, вытянутых вдоль экватора или какие-либо параллели. В навигации используется проекция Меркатора — равноугольная цилиндрическая проекция. Проекция Гаусса — Крюгера — равноугольная поперечно-цилиндрическая Картографические проекции — применяется при составлении топографических карт и обработке триангуляций.
Конические проекции (рис. 4) — проекции, в которых параллели изображаются концентрическими окружностями, меридианы — ортогональными им прямыми. В этих проекциях искажения не зависят от долготы. Особо пригодны для территорий, вытянутых вдоль параллелей. Карты всей территории СССР часто составляются в равноугольных и равнопромежуточных конических проекциях. Используются также как геодезические проекции.
Азимутальные проекции (рис. 5) — проекции, в которых параллели — концентрические окружности, меридианы — их радиусы, при этом углы между последними равны соответствующим разностям долгот. Частным случаем азимутальных проекций являются перспективные проекции.
Псевдоконические проекции (рис. 6) — проекции, в которых параллели изображаются концентрическими окружностями, средний меридиан — прямой линией, остальные меридианы — кривыми. Часто применяется равновеликая псевдоконическая проекция Бонна; в ней с 1847 составлялась трехверстная (1: 126 000) карта Европейской части России.
Псевдоцилиндрические проекции (рис. 8) — проекции, в которых параллели изображаются параллельными прямыми, средний меридиан — прямой линией, перпендикулярной этим прямым и являющейся осью симметрии проекций, остальные меридианы — кривыми.
Поликонические проекции (рис. 9) — проекции, в которых параллели изображаются окружностями с центрами, расположенными на одной прямой, изображающей средний меридиан. При построении конкретных поликонических проекций ставятся дополнительные условия. Одна из поликонических проекций рекомендована для международной (1: 1 000 000) карты.
Существует много проекций, не относящихся к указанным видам. Цилиндрические, конические и азимутальные проекции, называемые простейшими, часто относят к круговым проекциям в широком смысле, выделяя из них круговые проекции в узком смысле — проекции, в которых все меридианы и параллели изображаются окружностями, например конформные проекции Лагранжа, проекция Гринтена и др.
Использование и выбор картографических проекций зависят главным образом от назначения карты и ее масштаба, которыми часто обусловливается характер допускаемых искажений в избираемой Картографические проекции Карты крупных и средних масштабов, предназначенные для решения метрических задач, обычно составляют в равноугольных проекциях, а карты мелких масштабов, используемые для общих обозрений и определения соотношения площадей каких-либо территорий — в равновеликих. При этом возможно некоторое нарушение определяющих условий этих проекций (w º 0 или р º 1), не приводящее к ощутимым погрешностям, т. е. допустим выбор произвольных проекций, из которых чаще применяют проекции равнопромежуточные по меридианам. К последним прибегают и тогда, когда назначением карты вообще не предусмотрено сохранение углов или площадей. При выборе Картографические проекции начинают с простейших, затем переходят к более сложным проекциям, даже, возможно, модифицируя их. Если ни одна из известных Картографические проекции не удовлетворяет требованиям, предъявляемым к составляемой карте со стороны ее назначения, то изыскивают новую, наиболее подходящую Картографические проекции, пытаясь (насколько это возможно) уменьшить искажения в ней. Проблема построения наивыгоднейших Картографические проекции, в которых искажения в каком-либо смысле сведены до минимума, полностью еще не решена.
Картографические проекции используются также в навигации, астрономии, и др.; их изыскивают для целей картографирования Луны, планет и др. небесных тел.
Преобразование проекций. Рассматривая две Картографические проекции, заданные соответствующими системами уравнений: x = f1(j, l), y = f2(j, l) и X = g1(j, l), = g2(j, l), можно, исключая из этих уравнении j и l, установить переход от одной из них к другой:
Х = 1(x, у), = 2(x, у).
Эти формулы при конкретизации вида функций 1, 2, во-первых, дают общий метод получения так называемых производных проекций; во-вторых, составляют теоретическую основу всевозможных способов технических приемов составления карт (см. Географические карты). Например, аффинные и дробно-линейные преобразования осуществляются при помощи картографических трансформаторов. Однако более общие преобразования требуют применения новой, в частности электронной, техники. Задача создания совершенных трансформаторов Картографические проекции — актуальная проблема современной картографии.
Лит.: Витковский В., Картография. (Теория картографических проекций), СПБ. 1907; Каврайский В. В., Математическая картография, М. — Л., 1934; его же, Избр. труды, т. 2, в. 1—3, (М.), 1958—60; Урмаев Н. А., Математическая картография, М., 1941; его же, Методы изыскания новых картографических проекций, М., 1947; Граур А. В., Математическая картография, 2 изд., Л., 1956; Гинзбург Г. А., Картографические проекции, М., 1951; Мещеряков Г. А., Теоретические основы математической картографии, М., 1968.
Г. А. Мещеряков.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 00:07:48
|

|

|
 |
|

|
 |
 |
 |
|