|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Якоби многочлены | Якоби многочлены (далее Я), специальная система многочленов последовательно возрастающих степеней. Для n = 0,1,2...
Я Pn (a,b)(х) могут быть определены формулой:
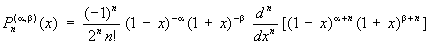
Я ортогональны на отрезке (—1,1) относительно веса (1—х)a (1 + х)b (см. Ортогональные многочлены). Введены К. Якоби (опубликовано в 1859). Частными случаями Я являются многочлены Лежандра (при a = b = 0), многочлены Чебышева первого рода (при a = b = —1/2) и второго рода (при a = b = 1/2), ультрасферические многочлены (при a = b). В свою очередь Я являются частным случаем гипергеометрической функции. Дифференциальное уравнение для у = Pn (a,b)(х):
 . |
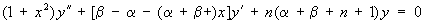Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.01.2025 23:08:43
|
|
|
|
|
|
|
|
|
|
|
