
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Эрмитов оператор | Эрмитов оператор (далее Э) бесконечномерный аналог эрмитова линейного преобразования (см. Эрмитова форма). Линейный ограниченный оператор А в комплексном гильбертовом пространстве и называется эрмитовым, если для любых двух векторов х и у этого пространства выполняется равенство (Ax, у) = (х, Ау), где (х, у) — скалярное произведение в Н. Примерами Э являются интегральные операторы (см. Интегральные уравнения), для которых ядро К (х, у) задано в ограниченной области и является непрерывной функцией такой, что 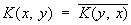 ; ;
в этом случае К (х, у) называется эрмитовым ядром. Понятие Э обобщается и на неограниченные линейные операторы в гильбертовом пространстве. Э играют значительную роль в квантовой механике, представляя удобный способ математического описания наблюдаемых величин, характеризующих физическую систему. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:57:03
|

|

|
 |
|

|
 |
 |
 |
|