|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Эрмитова форма | Эрмитова форма (далее Э) выражение вида
 ,
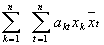где akt = atk (а - число, комплексносопряженное с а). Матрица, составленная из коэффициентов Э, называется эрмитовой; линейное преобразование, задаваемое эрмитовой матрицей, называется эрмитовым. Вопрос о представлении целых чисел Э при целочисленных значениях аргументов исследовал Ш. Эрмит (1854). Теория Э во многом аналогична теории квадратичных форм. См. также Эрмитов оператор. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 14:23:01
|
|
|
|
|
|
|
|
|
|
|
