|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Эрмита многочлены | Эрмита многочлены (далее Э) специальная система многочленов последовательно возрастающих степеней. Для n = 0,1,2,... Э n (x) могут быть определены формулой:
 .
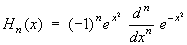В частности, o = 1, 1 = 2х. 2 = 4x2 — 2, 3 = 8x3 — 12x, 4 = 16х4 — 48х2 + 12. Э ортогональны на всей оси Ox относительно веса е-х (ортогональные многочлены). Дифференциальное уравнение для у = n (x).
y" — 2ху" + 2ny = 0;
рекуррентные формулы:
n+1 (х) — 2xHn (x) + 2nHn-1 (х) = 0,
 .
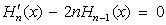Иногда за n принимают многочлены, отличающиеся от указанных выше множителями, зависящими от n, а иногда в качестве веса берут  . Основные свойства этой системы были изучены П. Л. Чебышевым (1859) и Ш. Эрмитом (1864). |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.12.2024 02:19:12
|
|
|
|
|
|
|
|
|
|
|
