
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Энтропия | Энтропия (далее Э) (от греч. entropía - поворот, превращение), понятие, впервые введенное в термодинамике для определения меры необратимого рассеяния энергии. Э широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации как мера неопределенности какого-либо опыта (испытания), который может иметь разные исходы. Эти трактовки Э имеют глубокую внутреннюю связь. Например, на основе представлений об информационной Э можно вывести все важнейшие положения статистической физики.
В термодинамике понятие "Э" было введено Р. Клаузиусом (1865), который показал, что процесс превращения теплоты в работу следует общей физической закономерности - второму началу термодинамики. Его можно сформулировать строго математически, если ввести особую функцию состояния - Э
Так, для термодинамической системы, совершающей квазистатически (бесконечно медленно) циклический процесс, в котором система последовательно получает малые количества теплоты dQ при соответствующих значениях абсолютной температуры Т, интеграл от "приведенного" количества теплоты dQ/ Т по всему циклу равен нулю
(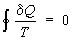 , т. н. равенство Клаузиуса). , т. н. равенство Клаузиуса).
Это равенство, эквивалентное второму началу термодинамики для равновесных процессов, Клаузиус получил, рассматривая произвольный циклический процесс как сумму очень большого, в пределе бесконечного, числа элементарных обратимых Карно циклов. Математически равенство Клаузиуса необходимо и достаточно для того, чтобы выражение
dS = dQ/T (1)
представляло собой полный дифференциал функции состояния , названное "Э" (дифференциальное определение Э). Разность Э системы в двух произвольных состояниях А и В (заданных, например, значениями температур и объемов) равна
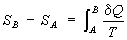 (2) (2)
(интегральное определение Э). Интегрирование здесь ведется вдоль пути любого квазистатического процесса, связывающего состояния А и В, при этом, согласно равенству Клаузиуса, приращение Э D = - A не зависит от пути интегрирования.
Т. о., из второго начала термодинамики следует, что существует однозначная функция состояния , которая при квазистатических адиабатных процессах (dQ = 0) остается постоянной. Процессы, в которых Э остается постоянной, называются изоэнтропийными. Примером может служить процесс, широко используемый для получения низких температур, - адиабатное размагничивание (см. Магнитное охлаждение). При изотермических процессах изменение Э равно отношению сообщенной системе теплоты к абсолютной температуре. Например, изменение Э при испарении жидкости равно отношению теплоты испарения к температуре испарения при условии равновесия жидкости с ее насыщенным паром.
Согласно первому началу термодинамики (закону сохранения энергии), dQ = dU+pdV, т. е. сообщаемое системе количество теплоты равно сумме приращения внутренней энергии dU и совершаемой системой работы pdV, где р - давление, - объем системы. С учетом первого начала термодинамики дифференциальное определение Э принимает вид
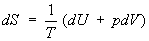 , (3) , (3)
откуда следует, что при выборе в качестве независимых переменных внутренней энергии и объема частные производные Э связаны с абсолютной температурой и давлением соотношениями:
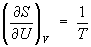 (4) и (4) и 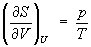 . (5) . (5)
Эти выражения представляют собой уравнения состояния системы (первое - калорическое, второе - термическое). Уравнение (4) лежит в основе определения абсолютной температуры (см. также Температура, Температурные шкалы).
Формула (2) определяет Э лишь с точностью до аддитивной постоянной (т. е. оставляет начало отсчета Э произвольным). Абсолютное значение Э позволяет установить третье начало термодинамики, или Нернста теорему: при стремлении абсолютной температуры к нулю разность D для любого вещества стремится к нулю независимо от внешних параметров. Поэтому: Э всех веществ при абсолютном нуле температуры можно принять равной нулю (эту формулировку теоремы Нернста предложил в 1911 М. Планк). Основываясь на ней, за начальную точку отсчета Э принимают o = 0 при Т = 0.
Важность понятия Э для анализа необратимых (неравновесных) процессов: также была показана впервые Клаузиусом. Для необратимых процессов интеграл от приведенной теплоты dQ / Т по замкнутому пути всегда отрицателен
(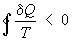 , т. н. неравенство Клаузиуса). , т. н. неравенство Клаузиуса).
Это неравенство - следствие теоремы Карно: кпд частично или полностью необратимого циклического процесса всегда меньше, чем кпд обратимого цикла. Из неравенства Клаузиуса вытекает, что
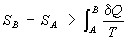 (6) (6)
поэтому Э адиабатически изолированной системы при необратимых процессах может только возрастать.
Т. о., Э определяет характер процессов в адиабатической системе: возможны только такие процессы, при которых Э либо остается неизменной (обратимые процессы), либо возрастает (необратимые процессы). При этом не обязательно, чтобы возрастала Э каждого из тел, участвующего в процессе. Увеличивается общая: сумма Э тел, в которых процесс вызвал изменения.
Термодинамическому равновесию адиабатической системы соответствует состояние с максимумом Э Э может иметь не один, а несколько максимумов, при этом система будет иметь несколько состояний равновесия. Равновесие, которому соответствует наибольший максимум Э, называется абсолютно устойчивым (стабильным). Из условия максимальности Э адиабатические системы в состоянии равновесия вытекает важное следствие: температура всех частей системы в состоянии равновесия одинакова.
Понятие "Э" применимо и к термодинамически неравновесным состояниям, если отклонения от термодинамического равновесия невелики и можно ввести представление о локальном термодинамическом равновесии в малых, но еще макроскопических объемах. Такие состояния можно охарактеризовать термодинамическими параметрами (температурой, давлением и т. д.), слабо зависящими от пространственных координат и времени, а Э термодинамически неравновесного состояния определить как Э равновесного состояния, характеризующегося теми же значениями параметров. В целом Э неравновесной системы равна сумме Э ее частей, находящихся в локальном равновесии.
Термодинамика неравновесных процессов позволяет более детально, чем классическая термодинамика, исследовать процесс возрастания Э и вычислить количество Э, образующейся в единице объема в единицу времени вследствие отклонения системы от термодинамического равновесия - производство энтропии. Производство Э всегда положительно и математически выражается квадратичной формой от градиентов термодинамических параметров (температуры, гидродинамической скорости или концентраций компонентов смеси) с коэффициентами, называемыми кинетическими (см. Онсагера теорема).
Статистическая физика связывает Э с вероятностью осуществления данного макроскопического состояния системы. Э определяется через логарифм статистического веса данного равновесного состояния
= k ln (E, ), (7)
где k - Больцмана постоянная, (E, ) - число квантовомеханических уровней в узком интервале энергии DЕ вблизи значения энергии Е системы из частиц. Впервые связь Э с вероятностью состояния системы была установлена Л. Больцманом в 1872: возрастание Э системы обусловлено ее переходом из менее вероятного состояния в более вероятное. Иными словами, эволюция замкнутой системы осуществляется в направлении наиболее вероятного распределения энергии по отдельным подсистемам.
В отличие от термодинамики статистическая физика рассматривает особый класс процессов - флуктуации, при которых система переходит из более вероятного состояния в менее вероятное, и ее Э уменьшается. Наличие флуктуаций показывает, что закон возрастания Э выполняется только в среднем для достаточно большого промежутка времени.
Э в статистической физике тесно связана с информационной Э, которая служит мерой неопределенности сообщений данного источника (сообщения описываются множеством величин х1, x2,..., xn, которые могут быть, например, словами какого-либо языка, и соответствующих вероятностей p1, p2,..., pn появления величин x1, x2,..., xn в сообщении). Для определенного (дискретного) статистического распределения вероятностей рк информационной Э называют величину
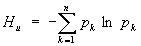
при условии
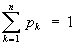 (8) (8)
Значение Ни равно нулю, если какое-либо из pk равно 1, а остальные - нулю, т. е. неопределенность в информации отсутствует. Э принимает наибольшее значение, когда pk равны между собой и неопределенность в информации максимальна. Информационная Э, как и термодинамическая, обладает свойством аддитивности (Э нескольких сообщений равна сумме Э отдельных сообщений). К. Э Шеннон показал, что Э источника информации определяет критическое значение скорости "помехоустойчивой" передачи информации по конкретному каналу связи (см. Шеннона теорема). Из вероятностной трактовки информационной Э могут быть выведены основные распределения статистической физики: каноническое Гиббса распределение, которое соответствует максимальному значению информационной Э при заданной средней энергии, и большое каноническое распределение Гиббса - при заданных средней энергии и числа частиц в системе.
Понятие Э, как показал впервые Э Шредингер (1944), существенно и для понимания явлений жизни. Живой организм с точки зрения протекающих в нем физико- процессов можно рассматривать как сложную открытую систему, находящуюся в неравновесном, но стационарном состоянии. Для организмов характерна сбалансированность процессов, ведущих к росту Э, и процессов обмена, уменьшающих ее. Однако жизнь не сводится к простой совокупности физико- процессов, ей свойственны сложные процессы саморегулирования. Поэтому с помощью понятия Э нельзя охарактеризовать жизнедеятельность организмов в целом.
Д. Н. Зубарев.
Э, характеризуя вероятность осуществления данного состояния системы, согласно (7) является мерой его неупорядоченности. Изменение Э D обусловлено как изменением р, и Т, так и процессами, протекающими при р, Т = const и связанными с превращением веществ, включая изменение их агрегатного состояния, растворение и взаимодействие.
Изотермическое сжатие вещества приводит к уменьшению, а изотермическое расширение и нагревание - к увеличению его Э, что соответствует уравнениям, вытекающим из первого и второго начал термодинамики (см. Термодинамика):
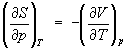 ; (9) ; (9)
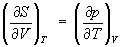 ; (10) ; (10) 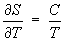 . (11) . (11)
Формулу (11) применяют для практического определения абсолютного значения Э при температуре Т, используя постулат Планка и значения теплоемкости С, теплот и температур фазовых переходов в интервале от 0 до Т К.
В соответствии с (1) Э измеряется в кал/(моль· К) (энтропийная единица - э. е.) и дж/(моль·К). При расчетах обычно применяют значения Э в стандартном состоянии, чаще всего при 298,15 К (25 °С), т. е. 0298; таковы приводимые ниже в статье значения Э
Э увеличивается при переходе вещества в состояние с большей энергией. D сублимации > DS парообразования >> DS плавления >DS полиморфного превращения. Например, Э воды в состоянии равна 11,5, в жидком - 16,75, в газообразном - 45,11 э. е.
Чем выше твердость вещества, тем меньше его Э; так, Э алмаза (0,57 э. е.) вдвое меньше Э графита (1,37 э. е.). Карбиды, бориды и другие очень твердые вещества характеризуются небольшой Э
Э аморфного тела несколько больше Э Возрастание степени дисперсности системы также приводит к некоторому увеличению ее Э
Э возрастает по мере усложнения молекулы вещества; так, для газов 2О, 23 и 25 Э составляет соответственно 52,6; 73,4 и 85,0 э. е. При одной и той же молекулярной массе Э разветвленных углеводородов меньше Э неразветвленных; Э циклоалкана (циклана) меньше Э соответствующего ему алкена.
Э простых веществ и соединений (например, ACIn), а также ее изменения при плавлении и парообразовании являются периодическими функциями порядкового номера соответствующего элемента. Периодичность изменения Э для сходных реакций типа 1/n Акрист + 1/2Сl2газ = 1/n ACln крист практически не проявляется. В совокупности веществ-аналогов, например АСl4газ (А - С, , , , ) Э изменяется закономерно. Сходство веществ (2 и СО; 2 и 2; 2 и 2; ВаСОз и 3; 4 и РЬМоО4) проявляется в близости их Э Выявление закономерности изменения Э в рядах подобных веществ, обусловленного различиями в их строении и составе, позволило разработать методы приближенного расчета Э
Знак изменения Э при реакции DS х. р. определяется знаком изменения объема системы DV х. р.; однако возможны процессы (изомеризация, циклизация), в которых DS х. р. ¹ 0, хотя DV х. р. " 0. В соответствии с уравнением DG = DН - ТDS (G - гиббсова энергия, Н - энтальпия) знак и абсолютное значение DS х. р. важны для суждения о влиянии температуры на равновесие химическое. Возможны самопроизвольные экзотермические. процессы (DG < 0, DH < 0), протекающие с уменьшением Э (DS < 0). Такие процессы распространены, в частности, при растворении (например, комплексообразование), что свидетельствует о важности взаимодействий между участвующими в них веществами.
М. X. Карапетьянц.
Лит.: Клаузиус ., в кн.: Второе начало термодинамики, М.-Л., 1934, с. 71-158; Зоммерфельд А., Термодинамика и статистическая физика, пер. с нем., М., 1955; Майер Дж., Гепперт-Майер М., Статистическая механика, пер. с англ., М., 1952; Де Гроот С., Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Яглом А. М., Яглом И. М., Вероятность и информация, 3 изд., М., 1973; Бриллюен Л., Наука и теория информации, пер. с англ., М., 1959. См. также лит. при ст. Термодинамика, Термодинамика неравновесных процессов и Статистическая физика. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 05:14:55
|

|

|
 |
|

|
 |
 |
 |
|