|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Элементарные делители | Элементарные делители (далее Э) квадратной матрицы А = ||aiK||1n, степени двучленов
(l - l1) p1, (l - l2) p2,..., (l - ls) ps,
которые получаются из характеристического уравнения
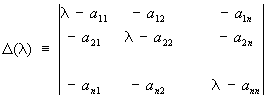
следующим образом. Миноры k-го порядка определителя D(l) (для k £ п) представляют собой многочлены относительно l. Пусть Dk (l) (k = 1, 2,..., n) - наибольший общий делитель всех этих многочленов, Dn (l) = D(l). В ряду каждый многочлен делится на предыдущий без остатка. Если разложить соответствующие частные на линейные множители в поле комплексных чисел:
.............................……………………………..,
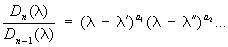
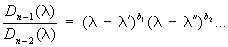
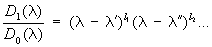
то степени 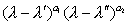 ,...,  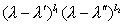,... и образуют полную систему Э матрицы А (при этом степени с нулевыми показателями не принимаются во внимание). Произведение всех Э равно характеристическому многочлену. Э определяют нормальную (жорданову) форму матрицы А. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.02.2025 02:34:01
|
|
|
|
|
|
|
|
|
|
|
