
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Электродинамика движущихся сред | Электродинамика движущихся сред (далее Э) раздел электродинамики, в котором изучаются электромагнитные явления, в частности законы распространения электромагнитных волн, в движущихся средах. Э включает также оптику движущихся сред, в которой исследуется распространение света в движущихся средах. Хотя экспериментальный материал накапливался в течение нескольких столетий, полное его объяснение стало возможным только после появления теории относительности.
18 и 19 вв. ознаменовались бурным развитием ньютоновской механики. На ее основе были объяснены не только механическое движение тел и динамика сплошных сред, но и, казалось бы, не связанные с механикой тепловые явления. У подавляющего большинства физиков возникла уверенность, что все явления в природе могут быть объяснены действием законов классической механики. Это нашло свое выражение и в подходе к электромагнитным явлениям. Опыты по интерференции света с неопровержимостью указывали на то, что свет имеет волновую природу. Но из механики было известно, что для распространения волны необходима упругая среда. Поэтому считалось, что и для распространения световых волн также нужна упругая среда. Колебания этой светоносной среды, названной эфиром, и связывались со световыми волнами. Т. к. было известно, что свет распространяется и в пустоте, приходилось считать, что пустота тоже заполнена световым эфиром. Эфир наделялся весьма необычными свойствами: с одной стороны, он должен был обладать очень большой упругостью (поскольку скорость распространения волн тем больше, чем больше упругость среды, а скорость световых волн очень велика), с другой — не должен оказывать никакого механического сопротивления движущимся сквозь него телам (поскольку все тела движутся в пустоте без сопротивления).
Попытка объяснения электромагнитных явлений с помощью теории эфира неизбежно приводила к вопросу о том, как протекают электромагнитные явления в теле, движущемся через эфир. Основные теории, созданные в конце 19 в. для описания оптических явлений в движущейся классической среде (теории Г. Герца и Х. Лоренца), базировались на представлении об эфире. Однако они противоречили некоторым известным к тому времени опытам.
Создание непротиворечивой Э стало возможным лишь после появления специальной теории относительности А. Эйнштейна (1905), которая устранила эфир как светоносную среду и как преимуществ. систему отсчета. Понятия "покоящаяся" и "движущаяся" среды потеряли свой абсолютный характер и стали определяться только выбором системы отсчета (и связанным с ней "наблюдателем").
В 1908 Г. Минковский показал, что Максвелла уравнения для покоящихся сред в сочетании с принципом относительности Эйнштейна (см. Относительности принцип) однозначно определяют электромагнитное поле в движущейся среде. Эти же уравнения могут быть получены и другим путем — усреднением микроскопических уравнений электронной теории Лоренца (см. Лоренца — Максвелла уравнения) с учетом того, что у всех частиц среды имеется скорость упорядоченного движения.
Уравнения для полей в движущейся среде совпадают с уравнениями Максвелла в покоящейся среде:
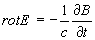 ; div D = 4pr; (1) ; div D = 4pr; (1)
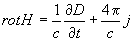 ; div = 0 ; div = 0
Здесь Е и Н — векторы напряженностей электрического и полей, D и В — электрическая и индукции, r и j — плотности внешних зарядов и токов.
Эта система уравнений должна быть дополнена т. н. материальными уравнениями, связывающими напряженности полей с индукциями. В покоящейся среде материальные уравнения имеют вид: D = eЕ, В = mН (1a), где e и m — диэлектрическая и проницаемости среды. Из вида этих соотношений в покоящейся среде однозначно следует их вид в среде, движущейся со скоростью u:
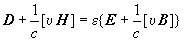 (2) (2)
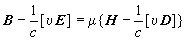
(квадратные скобки обозначают векторное произведение). Это т. н. материальные уравнения Минковского; при u= 0 они переходят в уравнения (1a). Материальные уравнения (2), вытекающие из принципа относительности, в сочетании с уравнениями Максвелла (1) удовлетворительно объясняют результаты всех экспериментов по изучению электромагнитных явлений в движущихся средах. Ниже рассмотрены некоторые из следствий теории Э
Распространение электромагнитных волн в движущейся среде. Пусть в среде, движущейся со скоростью u, распространяется электромагнитная волна
Е=Eoei (kr-wt), (3)
=oei (kr-wt).
Здесь Eo и Но — амплитуды электрического и полей, k — волновой вектор, w — круговая частота волны, r, t — координата и время. Из уравнений (1) — (3) вытекает, что волновой вектор и частота в движущейся среде связаны соотношением
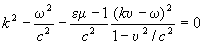 (4) (4)
При u = 0 (для покоящейся среды) получаем k2=emw2/c2. В соотношение (4) входит угол J между направлением распространения волны (вектором k) и скоростью u (ku = ku cos J); поэтому условия распространения волны для разных направлений различны. При малых u, ограничиваясь величинами первого порядка по u/c, из (4) можно получить выражение для фазовой скорости u фаз волны, распространяющейся под углом J к скорости среды:
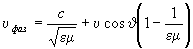 ; (5) ; (5)
направление фазовой скорости совпадает с направлением волнового вектора k. Эта формула была подтверждена в Физо опыте. Из (5), в частности, видно, что скорость света в движущейся среде не равна сумме скоростей света в неподвижной среде и самой среды.
Поляризация волны, т. е. направления векторов E0 и 0, зависит от скорости среды: вектор E0 перпендикулярен не k, как в покоящейся среде, а вектору
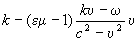 , (6) , (6)
представляющему собой линейную комбинацию скорости среды и волнового вектора; вектор 0 не перпендикулярен k и E0.
До сих пор предполагалось, что среда перемещается как целое равномерно и прямолинейно. Если скорость среды зависит от координат и времени, например если среда вращается, то методы специальной теории относительности становятся недостаточными для определения электромагнитного поля в этом случае. Вид уравнений поля может быть получен с помощью общей теории относительности. (При малых угловых скоростях вращения применима специальная теория относительности.)
Отражение и преломление света на движущихся границах раздела. Если электромагнитная волна падает на движущуюся границу раздела двух сред, то, как и в случае покоящейся границы, волна частично отражается, а частично проходит через границу. Однако движение границы приводит к ряду новых физических эффектов. Так, оказывается, что угол падения не равен углу отражения, а частоты всех трех волн — падающей, отраженной и преломленной — различны. Имеются и другие отличия: например, при некоторых скоростях границы может отсутствовать отраженная волна, но зато имеются две преломленные с разными частотами.
Рассмотрим простейший пример — отражение света от движущегося в пустоте зеркала (Эйнштейн, 1905). В этом случае прошедшая волна отсутствует, имеются лишь падающая и отраженная волны (рис. 1). Если скорость u зеркала направлена по нормали к его плоскости, а волна падает на зеркало под углом a1 к нормали, то угол отражения a2 след. образом выражается через угол падения:
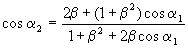 , (7) , (7)
где b = u/c (предполагается, что зеркало движется навстречу падающей волне). При b = 0 (зеркало покоится) получим cos a1 = cos a2, т. е. равенство углов падения и отражения. Напротив, если скорость зеркала стремится к скорости света, то из (7) следует, что при любом угле падения угол отражения равен нулю, т. е. даже при скользящем падении отраженная волна уходит от зеркала по нормали. Частота отраженной волны связана с частотой падающей волны соотношением:
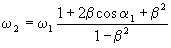 . (8) . (8)
Если волна падает на движущееся зеркало по нормали, то из (8) получается
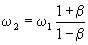 . (9) . (9)
Если скорость зеркала близка к скорости света, частота отраженной волны во много раз больше частоты падающей.
Движущееся зеркало — один из примеров движущейся границы раздела. В общем случае граница раздела не является идеально отражающей, поэтому кроме падающей и отраженной имеется преломленная волна. Помимо этого, и граница раздела, и среды по обе стороны от нее могут двигаться с различными скоростями. Если скорости сред по обе стороны от границы параллельны плоскости раздела, отражение волны от такой границы сопровождается поворотом плоскости поляризации, причем угол поворота пропорционален относит, скорости граничащих сред.
Для определения отраженной и преломленной волн необходимо знать условия, которым удовлетворяют поля на границе раздела. В системе отсчета, в которой граница раздела покоится, граничные условия оказываются такими же, как в электродинамике неподвижных тел.
По изменению частоты при отражении волны от движущейся границы может быть определена скорость границы. Было также предложено использовать этот эффект для умножения частоты электромагнитных волн; при этом в качестве отражающих тел предлагалось применять пучки ускоренной плазмы. Эксперимент подтвердил такую возможность, однако достигнутая эффективность преобразования частот пока невелика.
Излучение электромагнитных волн в движущейся среде. Источниками излучения в движущейся среде, как и в покоящейся, являются электрические заряды и токи. Однако характер распространения электромагнитных волн от источника, расположенного в движущейся среде, существенно отличается от того, что имеет место в случае покоящейся среды.
Пусть в некоторой малой области в движущейся среде расположен источник и время излучения мало. Если бы среда покоилась, то поле излучения расходилось бы от источника во все стороны с одинаковой скоростью, равной скорости света, т. е. все поле излучения было бы сосредоточено вблизи от сферической поверхности, расширяющейся со скоростью света. Движение среды приводит к тому, что скорость света в разных направлениях оказывается различной (см. формулу (5)). Поэтому поверхность, на которой поле излучения отлично от нуля, уже не является сферой. Расчет показывает, что эта поверхность имеет вид эллипсоида вращения с осью симметрии, направленной по скорости движения среды. Полуоси эллипса линейно растут со временем, а центр эллиптической оболочки перемещается параллельно скорости среды. Т. о., оболочка, на которой сосредоточено излучение, одновременно расширяется и "сносится по течению" в движущейся среде ("увлекается" средой). Если скорость перемещения среды сравнительно невелика, то источник излучения находится внутри этой оболочки (рис. 2).
Если же скорость движения среды превышает фазовую скорость света, то оболочку "сдувает" настолько сильно, что она вся оказывается "ниже по течению", и источник излучения находится вне этой оболочки (рис. 3).
Прохождение заряженной частицы через движущуюся среду. При рассмотрении излучения в движущейся среде ранее предполагалось, что источник излучения покоится. Если источник движется, то его поле излучения, как и в покоящейся среде, определяется интерференцией волн, испущенных источником в каждой точке своего пути. Отличие от случая покоящейся изотропной среды заключается в том, что из-за эффекта увлечения в движущейся среде скорость волн в разных направлениях различна (см. рис. 2 и 3).
Особенность излучения движущегося источника в движущейся среде можно понять на примере Черенкова — Вавилова излучения. Пусть в среде, движущейся со скоростью u, перемещается с постоянной скоростью и точечная заряженная частица. Для простоты будем считать, что и и u направлены по одной прямой. В случае покоящейся среды (u = 0) частица может стать источником излучения, если ее скорость достаточно велика (превышает фазовую скорость света в среде 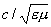 ). Возникающее излучение, называется излучением Черенкова — Вавилова, уносит энергию от движущейся частицы, которая, т. о., замедляется. В движущейся среде источником излучения Черенкова — Вавилова может быть медленная или даже покоящаяся заряженная частица. Если частица покоится, а скорость движения среды превышает фазовую скорость света, возникает характерное волновое поле, представляющее собой излучение Черенкова — Вавилова в этом случае. При этом на частицу — источник излучения — действует ускоряющая сила в направлении движения среды. ). Возникающее излучение, называется излучением Черенкова — Вавилова, уносит энергию от движущейся частицы, которая, т. о., замедляется. В движущейся среде источником излучения Черенкова — Вавилова может быть медленная или даже покоящаяся заряженная частица. Если частица покоится, а скорость движения среды превышает фазовую скорость света, возникает характерное волновое поле, представляющее собой излучение Черенкова — Вавилова в этом случае. При этом на частицу — источник излучения — действует ускоряющая сила в направлении движения среды.
Рассмотренный пример показывает, что в движущейся среде характер взаимодействия заряженной частицы со средой меняется. В зависимости от скоростей частицы и среды потери энергии частицы могут иметь различную величину и даже менять знак, что соответствует уже не замедлению, а ускорению частицы средой.
После того как стали получать (с помощью сильноточных и плазменных ускорителей) пучки заряженных частиц большой плотности движущиеся с релятивистской скоростью интерес к Э возрос. Плотные пучки во многих отношениях ведут себя как макроскопическая движущаяся среда В связи с применением таких пучков появились новые возможности не только в Э вообще, но также в изучении эффектов выше 1-го порядка по u/c, т. е. эффектов в которых величина u/c уже не мала по сравнению с единицей.
Лит.: мм И. Е. Основы теории электричества, 9 изд., М., 1976; его же, Собр. научных трудов, т. 1, М., 1975; Беккер Р., Электронная теория, пер. с нем., Л. — М., 1936; Болотовский Б. М., Столяров С. С., Современное состояние электродинамики движущихся сред (безграничные среды), в кн.: Эйнштейновский сборник. 1974, М., 1976.
Б. М. Болотовский.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 05:00:51
|

|

|
 |
|

|
 |
 |
 |
|