|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Эйри функции | Эйри функции (далее Э) функции Ai (z) и (z), являющиеся решениями дифференциального уравнения 2-го порядка
" - zW = 0
(z - независимое переменное). Э от аргумента (-z) выражаются через Бесселя функции индекса n = ± 1/3:
 ,
 ,
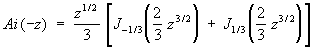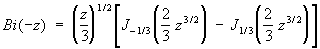½arg z½ < 2p/3.
Асимптотические представления для больших ½z½:
 ,
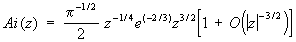½arg z½ £ 2p/3¾d,
 ,
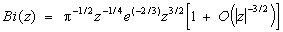½arg z½£ p/3¾d.
Э играют важную роль в теории асимптотических представлений различных специальных функций; находят разнообразные применения в математической физике, например в теории дифракции радиоволн у земной поверхности. Рассмотрены Дж. Р. Эйри (J. R. Airey, 1911).
Лит.: Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М.- JI., 1963.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 28.02.2025 20:39:24
|
|
|
|
|
|
|
|
|
|
|
