
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Эйлеровы интегралы | Эйлеровы интегралы (далее Э) интегралы вида
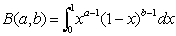 (1) (1)
(Э первого рода, или бета-функция, изученная Л. Эйлером в 1730—31, ранее рассматривалась И. Ньютоном и Дж. Валлисом) и
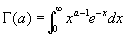 (2) (2)
(Э второго рода, или гамма-функция, рассмотренная Л. Эйлером в 1729—30 в форме, эквивалентной формуле (2); сама формула (2) встречается у Эйлера в 1781); название "Э" дано А. Лежандром. Э позволяют обобщить на случай непрерывно изменяющихся аргументов биномиальные коэффициенты 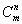 и факториал n!, ибо, если а и b— натуральные числа, то и факториал n!, ибо, если а и b— натуральные числа, то
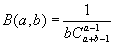 , Г (а +1) = а! , Г (а +1) = а!
Интегралы (1) и (2) абсолютно сходятся, если а и b положительны, и перестают существовать, если а и b отрицательны. Имеют место соотношения
В (a, b) = (b, a), 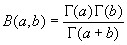 ; ;
последнее сводит бета-функцию к гамма-функции. Существует ряд соотношений между Э при различных значениях аргумента, обобщающих соответствующие соотношения между биномиальными коэффициентами. Э можно рассматривать и при комплексных значениях аргументов а и b. Э встречаются во многих вопросах теории специальных функций, к ним сводятся многие определенные интегралы, не выражаемые элементарно. Э называется также интеграл
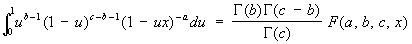
выражающий т. н. гипергеометрическую функцию.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969; Артин Е., Введение в теорию гамма-функций, пер. с нем., М.— Л., 1934; Уиттекер Е. Т., Ватсон Д. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 04:55:22
|

|

|
 |
|

|
 |
 |
 |
|