
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Эйлерова характеристика | Эйлерова характеристика (далее Э) многогранника, число ao-a1 +a2, где ao - число вершин, a1 - число ребер и a2- число граней многогранника. Если многогранник выпуклый или гомеоморфен (см. Гомеоморфизм) выпуклому, то его Э равна двум (теорема Л. Эйлера, 1758, известная еще Р. Декарту).
Э произвольного комплекса есть число 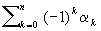 , где n - размерность комплекса, ao - число его вершин, a1 - число его ребер, вообще ak есть число входящих в комплекс k-мерных симплексов. Оказывается, что Э равна , где n - размерность комплекса, ao - число его вершин, a1 - число его ребер, вообще ak есть число входящих в комплекс k-мерных симплексов. Оказывается, что Э равна 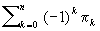 (формула Эйлера-Пуанкаре), где pk есть k-мерное число Бетти данного комплекса (см. Топология). Отсюда следует топологическая инвариантность Э Ввиду топологической инвариантности Э говорят об Э поверхности, а также полиэдра, подразумевая под этим Э любой триангуляции этой поверхности (этого полиэдра). (формула Эйлера-Пуанкаре), где pk есть k-мерное число Бетти данного комплекса (см. Топология). Отсюда следует топологическая инвариантность Э Ввиду топологической инвариантности Э говорят об Э поверхности, а также полиэдра, подразумевая под этим Э любой триангуляции этой поверхности (этого полиэдра).
Лит.: Александров П. С., Комбинаторная топология, М.- Л., 1947; Понтрягин Л. С., Основы комбинаторной топологии. 2 изд., М., 1976.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 06:18:15
|

|

|
 |
|

|
 |
 |
 |
|