
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Эйлера числа | Эйлера числа (далее Э) в математике, целые числа Еп, являющиеся коэффициентами при tn/n!, в разложении функции 1/cht (см. Гиперболические функции) в степенной ряд:
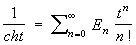
Введены Л. Эйлером в 1755. Э связаны рекуррентным соотношением (Е+1) n+(E¾1) n = 0, n = 1, 2, 3,..., E0 = 1 (после возведения в степень надо вместо Ek подставить Ek) и с Бернулли числами — соотношениями
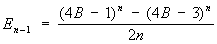 , ,
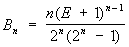 и и 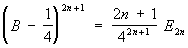 . .
Встречаются в различных формулах математического анализа.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 05:00:33
|

|

|
 |
|

|
 |
 |
 |
|