
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Эйлера уравнение | Эйлера уравнение (далее Э)
1) дифференциальное уравнение вида
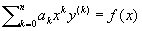 , (*) , (*)
где ao,..., an—постоянные числа; при х>0 уравнение (*) подстановкой х = et сводится к линейному дифференциальному уравнению с постоянными коэффициентами. Изучалось Л. Эйлером с 1740. К уравнению (*) сводится подстановкой x" = ax + b уравнение
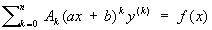 . .
2) Дифференциальное уравнение вида
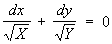 , ,
где X (x) = a0x4 + a1x3 + a2x2 + a3x + a4, (y) = а0у4+а1у3+а2у2+а3у +a4. Л. Эйлер рассматривал это уравнение в ряде работ начиная с 1753. Он показал, что общее решение этого уравнения имеет вид (х, у) = 0, где (х, у) — симметричный многочлен четвертой степени от х и у. Этот результат Эйлера послужил основой теории эллиптических интегралов.
3) Дифференциальное уравнение вида
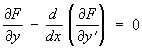 " "
служащее в вариационном исчислении для разыскания экстремалей интеграла
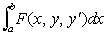 . .
Выведено Л. Эйлером в 1744.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 07:38:05
|

|

|
 |
|

|
 |
 |
 |
|