|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Эйлера-Маклорена формула | Эйлера—Маклорена формула (далее Э)формула суммирования, связывающая частные суммы ряда с интегралом и производными его общего члена:
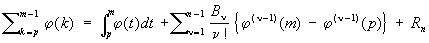
где v—Бернулли числа, Rn — остаточный член. Э.—М. ф. применяется для приближенного вычисления определенных интегралов, для исследования сходимости рядов, для вычисления сумм и для разложения функций в ряд Тейлора. Например, при m = 1, р = 0, n = 2m + 1,
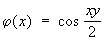
Э. — М. ф. дает следующее выражение:
 .
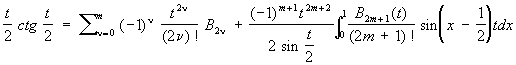Э.—М. ф. была впервые приведена Л. Эйлером в 1738. Независимо формула была открыта позднее К. Маклореном (1742).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 12:12:15
|
|
|
|
|
|
|
|
|
|
|
