
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Эволюта и эвольвента | Эволюта и эвольвента (далее Э)(от лат. evolutus — развернутый и evolvens, род. падеж evolventis — разворачивающий), понятия дифференциальной геометрии: множество m центров кривизны плоской кривой l называется эволютой этой кривой; кривая l по отношению к своей эволюте называется эвольвентой (см. рис.). Эвольвента l кривой m может быть получена как траектория конца В нити AB, которая наматывается на линию m или разматывается с нее (этим построением эвольвенты и объясняется др. ее назв. "развертка"). Указанное построение эвольвенты делает ясным следующие свойства Э. и э.: 1) касательная CD в произвольной точке С эволюты является нормалью в соответствующей точке D эвольвенты (следовательно, эвольвента есть ортогональная траектория касательных эволюты); 2) всякая ортогональная траектория касательных кривой т является эвольвентой (поэтому у данной кривой бесконечно много эвольвент); 3) разность радиусов кривизны AB и CD в точках В и D эвольвенты равна длине дуги AC эволюты; 4) эволюта является огибающей семейства нормалей эвольвенты.
Если линия l задана параметрическими уравнениями х = x (t), y = y (t), то параметрические уравнения ее эволюты будут следующие:
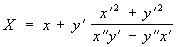 , ,
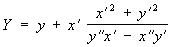
Эвольвенту пространственной кривой можно определить как ортогональную траекторию касательных этой кривой.
Лит.: Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 04:56:50
|

|

|
 |
|

|
 |
 |
 |
|