
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Штрафных функций метод | Штрафных функций метод (далее Ш) метод сведения задач об отыскании условного (относительного) экстремума функций к задачам отыскания безусловного (абсолютного) экстремума. Рассмотрим Ш на примере задач математического программирования. Пусть требуется минимизировать функцию j(х) на множестве X = {x: fi (x) ³ 0, = 1, 2,... m} n-мерного евклидова пространства. Штрафной функцией, или штрафом (за нарушение ограничений fi (x) ³ 0, i = 1, 2,... m), называют функцию y (х, а), зависящую от х и числового параметра а > 0, обладающую след. свойствами: y(х, а) = 0, если х Î Х и y(х, а) > 0, если x Ï X. Построим функцию M (x, a) = j(x) + y(х, a) и обозначим через x (a) любую точку ее безусловного глобального минимума. Пусть 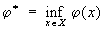 . Функцию y(х, a) выбирают таким образом, чтобы j(x (a*(® j* при a ® +¥. В качестве j(х, a) часто выбирают функцию . Функцию y(х, a) выбирают таким образом, чтобы j(x (a*(® j* при a ® +¥. В качестве j(х, a) часто выбирают функцию
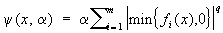 , q ³ 1. , q ³ 1.
Выбор конкретного вида функции y(x, a) связан как с проблемой сходимости Ш, так и с проблемами, возникающими при решении задачи безусловной минимизации функции М (х, a).
В несколько более общей постановке Ш заключается в сведении задачи минимизации функции j(х) на множестве Х к задаче минимизации некоторой параметрической функции М (х, a) на множестве более простой структуры с точки зрения эффективности применения численных методов минимизации, чем исходное множество X.
Лит.: Моисеев Н. Н., Элементы теории оптимальных систем, М., 1975; Фиакко А., Мак-Кормик Г., Нелинейное программирование, пер. с англ., М., 1972; Сеа Ж., Оптимизация, пер. с франц., М., 1973.
В. Г. Карманов.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:51:38
|

|

|
 |
|

|
 |
 |
 |
|