
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Четырехмерный интервал | Четырехмерный интервал (далее Ч)интервал, в теории относительности — величина, характеризующая связь между пространственным расстоянием и промежутком времени, разделяющими 2 события. С математической точки зрения интервал есть "расстояние" между двумя событиями в четырехмерном пространстве-времени.
В специальной (частной) теории относительности квадрат Четырехмерный интервал (sAB) между двумя событиями А и В равен:
s2ab = c2(Dt)2 ( (Dr)2,
где Dt и Dr — соответственно промежуток времени и пространственное расстояние между этими событиями, с — скорость света в вакууме. Интервал между событиями остается неизменным при переходе от одной инерциальной системы отсчета к другой, т. е. инвариантен относительно Лоренца преобразований (в то время как величины Dr и Dt зависят от выбора системы отсчета). Если s2AB >0, то интервал называется времениподобным; в этом случае существует система отсчета, в которой события происходят в одной пространственной точке (Dr = 0) и sab = cDt, т. е. интервал равен промежутку времени между событиями в этой системе, умноженному на скорость света.
Если 2AB<0, то интервал называется пространственноподобным; в этом случае существует система отсчета, в которой события происходят одновременно (Dt = 0) и расстояние между ними Dr = = iSAB, где
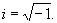
При sab = 0 интервал называется нулевым; в этом случае Dr = cDt всегда, т. е. события в любой системе отсчета могут быть связаны световым сигналом (см. Относительности теория).
В общей теории относительности, рассматривающей искривленное пространство-время при наличии тяготения, все сказанное об интервале справедливо для бесконечно близких событий (см. Тяготение).
И. Д. Новиков.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 13.03.2026 01:07:59
|

|

|
 |
|

|
 |
 |
 |
|