
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Бесселя функции | Бесселя функции (далее Б) цилиндрические функции 1-го рода; возникают при рассмотрении физических процессов (теплопроводности, диффузии, колебаний и пр.) в областях с круговой и цилиндрической симметрией; являются решениями Бесселя уравнения.
Б Jp порядка (индекса) р, - ¥ < p < ¥, представляется рядом
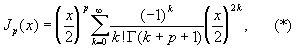
сходящимся при всех х. Ее график при х > 0 имеет вид затухающего колебания; Jp (x) имеет бесчисленное множество нулей; поведение Jp (x) при малых |х| дается первым слагаемым ряда (*), при больших х > 0 справедливо асимптотическое представление
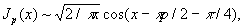
в котором отчетливо проявляется колебательный характер функции. Б "полуцелого" порядка р = n + 1/2 выражаются через элементарные функции; в частности,
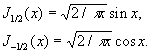
Б Jp (mpnx/l) (где mpn - положительные нули Jp (x), р > -1/2) образуют ортогональную с весом х в промежутке (0, l) систему (см. Ортогональная система функций).
Функция J0 была впервые рассмотрена Д. Бернулли в работе, посвященной колебанию тяжелых цепей (1732). Л. Эйлер, рассматривая задачу о колебаниях круглой мембраны (1738), пришел к уравнению Бесселя с целыми значениями р = n и нашел выражение J„(x) в виде ряда по степеням х. В последующих работах он распространил это выражение на случай произвольных значений р. Ф. Бессель исследовал (1824) функции Jp (x) в связи с изучением движения планет вокруг Солнца. Он составил первые таблицы для J0(x), J1(x), J2(x).
Лит.: Ватсон Г. Н., Теория бесселевых функций, пер. с англ., ч. 1-2, М., 1949; Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М.- Л., 1963; Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, функции Бесселя, функции параболического цилиндра, ортогональные многочлены, пер. с англ., М., 1966.
П. И. Лизоркин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.02.2026 03:51:03
|

|

|
 |
|

|
 |
 |
 |
|