
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Бесселя неравенство | Бесселя неравенство (далее Б) неравенство для коэффициентов ряда Фурье (см. Фурье ряд) по произвольной ортонормированной системе функций jk (x) (k = 1, 2...), т. е. системе, определенной на некотором отрезке (а, b) и удовлетворяющей условиям (k ¹ l)
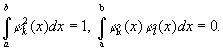
Если функция f (x) измерима на отрезке (а, b), а функция f2(x) интегрируема на этом отрезке и
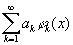
— ряд Фурье f (x) по системе jk (x), то справедливо Б
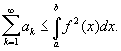
Б играет важную роль во всех исследованиях, относящихся к теории ортогональных рядов. В частности, оно показывает, что коэффициенты Фурье функции f (x) стремятся к нулю при n ® ¥. Для тригонометрической системы функций это неравенство было получено Ф. Бесселем (1828). Если система функций jk такова, что для любой функции f Б обращается в равенство, то оно называется Парсеваля равенством.
С. Б. Стечкин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.02.2026 02:05:44
|

|

|
 |
|

|
 |
 |
 |
|