
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Бесконечно малая | Бесконечно малая (далее Б) в математике, переменная величина, стремящаяся к пределу, равному нулю. Для того чтобы понятие Б имело точный смысл, необходимо указывать тот процесс изменения, при котором данная величина становится Б Например, величина y = 1/x является Б при аргументе х, стремящемся к бесконечности, а при х, стремящемся к нулю, она оказывается бесконечно большой. Если предел переменной у конечен и равен а, то lim (y - a) = 0 и обратно. Поэтому понятие Б величины можно положить в основу общего определения предела переменной величины. Теория Б является одним из способов построения теории пределов.
При рассмотрении нескольких переменных величин, участвующих в одном и том же процессе изменения, переменные у и z называются эквивалентными, если limz/y = 1; если при этом у является Б, то у и z называются эквивалентными Б Переменная z называется Б относительно у, если z/y есть Б Последний факт часто записывается в виде z = о (у) (читается: "z есть о малое от у"). Если при этом у является Б, то говорят, что z есть Б более высокого порядка, чем у. Часто среди нескольких Б, участвующих в одном и том же процессе изменения, одна из них, скажем у, принимается за главную, и с ней сравниваются все остальные. Тогда говорят, что z есть Б порядка k > 0, если предел lim z/ук существует и отличен от нуля; если же этот предел равен нулю, то z называется Б порядка выше k. Изучение порядков различного рода Б — одна из важных задач математического анализа.
Для случая, когда переменная величина есть функция аргумента х, из общего определения предела вытекает такое развернутое определение Б: функция f (x), определенная в окрестности точки x0, называется Б при х, стремящемся к x0, если для любого положительного числа e найдется такое положительное число d, что для всех x ¹ x0, удовлетворяющих условию |x - x0| < d, выполняется неравенство |f (x)| < e. Этот факт записывается в виде
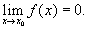
При изучении функции f (x) вблизи точки xo за главную Б принимают приращение независимого переменного Dх = х - х0. Формула
Dy = f`(x0) Dx + о (Dх)
выражает, например, что приращение Dy дифференцируемой функции с точностью до Б порядка выше первого совпадает с ее дифференциалом dy = f " (x0) Dx.
Метод Б, или (что то же) метод пределов, является в настоящее время основным методом обоснования математического анализа, почему его и называют также анализом Б Он заменил исчерпывания метод древних и "неделимых" метод. Метод Б был намечен И. Ньютоном (1666) и получил всеобщее признание после работ О. Коши. При помощи Б даются определения таких основных понятий анализа, как сходящийся ряд, интеграл, производная, дифференциал. Кроме того, метод Б служит одним из основных методов приложения математики к задачам естествознания. Это связано с тем, что большинство закономерностей механики и классической физики выражается в виде формул, связывающих Б приращения изучаемых величин, и обращение к Б является обычным приемом составления дифференциальных уравнений задачи.
Лит. см. при ст. Анализ математический.
С. Б. Стечкин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.02.2026 02:07:23
|

|

|
 |
|

|
 |
 |
 |
|