
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Бесконечное произведение | Бесконечное произведение (далее Б)произведение бесконечного числа сомножителей u1, u2,..., un,..., т. е. выражение вида

Бесконечное произведение, в котором сомножителями являются числа, иногда называемые бесконечным числовым произведением. Бесконечное произведение не всегда может быть приписано числовое значение. Если существует отличный от нуля предел последовательности частичных произведений
pn = u1 u2... un
при n ® ¥, то Бесконечное произведение называется сходящимся, a lim pn = р - его значением, и пишут:
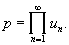
Исторически Бесконечное произведение впервые встретились в связи с задачей о вычислении числа p. Так, французский математик Ф. Виет (16 в.) получил формулу:
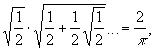
а английский математик Дж. Валлис (17 в.) - формулу:
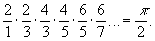
Особое значение Бесконечное произведение приобрели после работ Л. Эйлера, применившего Бесконечное произведение для изображения функций. Примером может служить разложение синуса:
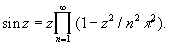
Разложения функций в Бесконечное произведение аналогичны разложениям многочленов на линейные множители; они замечательны тем, что выявляют все значения независимого переменного, при которых функция обращается в нуль.
Для сходимости Бесконечное произведение необходимо и достаточно, чтобы un ¹ 0 для всех номеров n, чтобы u > 0, начиная с некоторого номера , и чтобы сходился ряд
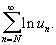
Т. о., исследование сходимости Бесконечное произведение эквивалентно исследованию сходимости этого ряда.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, т. 2, М.- Л., 1966; Ильин В. А., Позняк Э. Г., Основы математического анализа, М., 1965. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.02.2026 02:05:36
|

|

|
 |
|

|
 |
 |
 |
|