
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Бесконечно большая | Бесконечно большая (далее Б) в математике, переменная величина, которая в данном процессе изменения становится и остается по абсолютной величине больше любого наперед заданного числа. Изучение Б величин может быть сведено к изучению бесконечно малых, т.к. если у есть Б величина, то обратная ей величина z = 1/y является бесконечно малой. Тот факт, что переменная у является Б, записывают в виде lim y = ¥. При этом символ¥ ("бесконечность") является просто условным обозначением того, что у есть Б величина. Возможна и др. точка зрения, в силу которой ¥ является несобственным элементом, присоединяемым к множеству действительных чисел (см. Бесконечность в математике). Применительно к функции аргумента х развернутое определение Б звучит так: функция f (x), определенная в окрестности точки х0, называется Б при х, стремящемся к х0, если для любого числа > 0 найдется такое число d>0, что для всех x ¹ x0 и таких, что |х - х0| < d, выполняется неравенство |f (x)| > . Это свойство записывается в виде
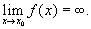
С. Б. Стечкин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.02.2026 02:07:06
|

|

|
 |
|

|
 |
 |
 |
|