
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Чебышева неравенство | Чебышева неравенство (далее Ч)
1) одно из основных неравенств для монотонных последовательностей или функций. В случае конечных последовательностей
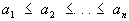
и
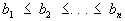
оно имеет вид:
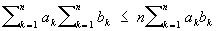
а в интегральной форме ¾ вид:
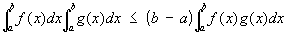 , ,
где f (x) ³ 0, g (x) ³ 0 и обе функции либо убывают, либо возрастают. Ч установлено П. Л. Чебышевым (1882).
2) Неравенство, дающее оценку вероятности того, что отклонение случайной величины от ее математического ожидания превзойдет некоторую заданную границу. Пусть x — какая-либо случайная величина, Ex = a — ее математическое ожидание, а Dx = s2 ¾ ее дисперсия. Тогда Ч утверждает, что вероятность неравенства | x ¾ a |³ k s не превосходит величины 1/k2. Если x — сумма независимых случайных величин, то при некоторых дополнительных ограничениях оценка 1/k2 может быть заменена оценкой
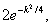
убывающей с ростом k значительно быстрее.
Свое название Ч получило по имени П. Л. Чебышева, который с его помощью установил (1867) весьма широкие условия приложимости закона больших чисел к суммам независимых случайных величин. См. Больших чисел закон, Предельные теоремы теории вероятностей.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 13.03.2026 01:11:09
|

|

|
 |
|

|
 |
 |
 |
|