
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Чебышева многочлены | Чебышева многочлены (далее Ч)
1) Ч 1-го рода - специальная система многочленов последовательно возрастающих степеней. Для n = 0, 1, 2,... определяются формулой:
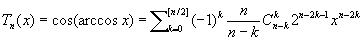
В частности, Т0 = 1; T1 = х; T2 = 2x2 ¾1; T3 = 4x3 ¾ 3x; T4 = 8x4 ¾ 8x2 + 1. Ч Tn (x) ортогональны (см. Ортогональные многочлены) на отрезке (-1; + 1) относительно веса (1 - x2)¾1/2. Дифференциальное уравнение:
(1 - x2) у" - ху + n2у = 0.
Рекуррентная формула: Tn+1(x) = 2xTn (х) - Tn¾1(x).
Ч 1-го рода являются частным случаем Якоби многочленов n (ab)(x):
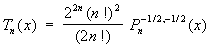 . .
2) Ч 2-го рода n (x) - ортогональная на отрезке (-1; + 1) относительно веса (1 -x2)1/2 система многочленов, связанная с Ч 1-го рода, например рекуррентным соотношением:
(1 - x2) n¾1(х) = xTn (х) ¾ Tn+1(х).
Лит.: Чебышев П. Л., Полн. собр. соч., т. 2-3, М.-Л., 1947-48; Сеге Г., Ортогональные многочлены, пер. с англ., М., 1962.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:52:31
|

|

|
 |
|

|
 |
 |
 |
|