
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Чаплыгина метод | Чаплыгина метод (далее Ч) метод приближенного интегрирования дифференциальных уравнений, предложенный С. А. Чаплыгиным (1919). Ч позволяет приближенно решать дифференциальное уравнение с заранее заданной степенью точности путем построения последовательности функций {un} и {vn}, все более точно аппроксимирующих искомое решение у заданного дифференциального уравнения и таких, что un ³ un+1 ³ у ³ vn+1 ³ vn. Способ построения последовательностей {un} и {vn} основан на теореме Чаплыгина о дифференциальных неравенствах и представляет собой обобщение на случай дифференциальных уравнений известного Ньютона метода, причем имеет место та же скорость сходимости, что и в методе Ньютона, т. е. погрешность имеет порядок 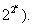
Лит.: Чаплыгин С. А., Новый метод приближенного интегрирования дифференциальных уравнений, М.—Л., 1950.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 13.03.2026 20:07:54
|

|

|
 |
|

|
 |
 |
 |
|