
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Циркуляция скорости | Циркуляция скорости (далее Ц) кинематическая характеристика течения жидкости или газа, которая служит мерой завихренности течения. Если скорости всех жидких частиц, расположенных на некоторой замкнутой кривой длиной l, направлены по касательной к этой кривой и имеют одну и ту же численную величину v, то Ц определяется равенством Г = ul. Такой случай имеет место для прямолинейного вихря, т. е. плоскопараллельного течения жидкости, при котором все ее частицы движутся по концентрическим окружностям с центрами на оси вихря (жидкость как бы "вращается" вокруг этой оси). В общем случае
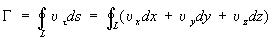 , ,
где криволинейный интеграл берется по замкнутой кривой L, ut — проекция скорости на касательную к этой кривой, ds — элемент длины кривой, ux, uy, uz — проекции скорости на координатные оси, х, у, z — координаты точек кривой.
Если Ц по любому замкнутому контуру, проведенному внутри жидкости, равна нулю, то течение жидкости будет безвихревым или потенциальным течением и потенциал скоростей будет однозначной функцией координат. Если же Ц по некоторым контурам будет отлична от нуля, то течение жидкости будет либо вихревым в соответственных областях, либо безвихревым, но с неоднозначным потенциалом скоростей (область течения неодносвязна, т. е. в ней имеются замкнутые твердые границы, например быки моста в реке). В последнем случае Ц по всем контурам, охватывающим одни и те же границы, имеет одно и то же значение. Ц широко используется как характеристика течений идеальной (без учета вязкости) жидкости (см., например, в Жуковского теореме). Для вязкой жидкости Ц всегда отлична от нуля и со временем изменяется вследствие диффузии вихрей.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 18:49:23
|

|

|
 |
|

|
 |
 |
 |
|