
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Бернулли числа | Бернулли числа (далее Б) специальная последовательность рациональных чисел, фигурирующая в различных вопросах математического анализа и теории чисел. Значения первых шести Б:
1 = 1/6, 2 = 1/30, 3 = 1/42, 4 = 1/30,
5 = 5/66, 6 = 691/2730.
В математическом анализе Б появляются как коэффициенты разложения некоторых элементарных функций в степенные ряды. Например:
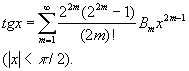
К числу важнейших формул, в которых встречаются Б, относится формула суммирования Эйлера — Маклорена (см. Конечных разностей исчисление). Через Б выражаются суммы многих рядов и значения несобственных интегралов. Б впервые появились в посмертной работе Я. Бернулли (1713) в связи с вычислением суммы одинаковых степеней натуральных чисел. Он доказал, что
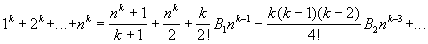
Для Б известны рекуррентные формулы, позволяющие последовательно вычислять эти числа, а также явные формулы (имеющие довольно сложный вид).
Большой интерес представляют теоретико-числовые свойства Б Немецкий математик Э. Куммер в 1850 установил, что уравнение Ферма xp + ур = zp не решается в целых числах х, у, z, отличных от нуля, если простое число р > 2 не делит числителей Б 1, 2,... (p - 3)/2. Нередко для обозначения Б вместо m пишут (-1) m - 12m (m = 1, 2...); кроме того, полагают
0 = 1, 1 = - 1/2,
3 = 5 = 7 =... = 0.
Лит.: Чистяков И. И., Бернуллиевые числа, М., 1895; Кудрявцев В. А., Суммирование степеней чисел натурального ряда и числа Бернулли, М.—Л., 1936; Уиттекер Э.-Т. и Ватсон Д.-Н., Курс современного анализа, пер. с англ., 2 изд., ч. 1, М., 1963; Landau Е., Vorlesungen über Zahlentheorie, Bd 3, . ., 1927.
С. Б. Стечкин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.02.2026 03:54:15
|

|

|
 |
|

|
 |
 |
 |
|