
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Цилиндрические функции | Цилиндрические функции (далее Ц)весьма важный с точки зрения приложений в физике и технике класс трансцендентных функций, являющихся решениями дифференциального уравнения:
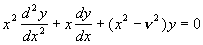 (1) (1)
где n - произвольный параметр. К этому уравнению сводятся многие вопросы равновесия (упругого, теплового, электрического) и колебаний тел цилиндрической формы. Решение, имеющее вид:
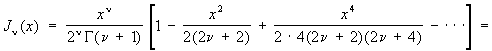 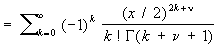
(где Г (z) - гамма-функция; ряд справа сходится при всех значениях х), называется Цилиндрические функции первого рода порядка n. В частности, Цилиндрические функции нулевого порядка имеет вид:
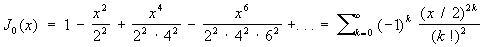
Если n - целое отрицательное: n = - n, то Jn(x) определяется так:
J-n (x) = (- 1) n Jn (x).
Цилиндрические функции порядка n = m + 1/2, где m - целое число, сводится к элементарным функциям, например:
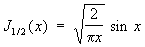 , , 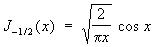
Функции Jn(x) и уравнение (1) называют также по имени Ф. Бесселя (Бесселя функции, Бесселя уравнение). Однако эти функции и уравнение (1) были получены еще Л. Эйлером при изучении колебаний мембраны в 1766, т. е. почти за 50 лет до работ Бесселя; функция нулевого порядка встречается еще раньше в работе Д. Бернулли, посвященной колебанию тяжелой цепи (опубликована в 1738), а функция порядка 1/3 в письме Я. Бернулли к Г. Лейбницу (1703).
Если n не является целым числом, то общее решение уравнения (1) имеет вид
y = 1Jn(x) + 2J-n(x), (2)
где 1 и 2 - постоянные. Если же n - целое, то Jn(x) и J-n(x) линейно зависимы, и их линейная комбинация (2) уже не является общим решением уравнения (1). Поэтому, наряду с Цилиндрические функции первого рода, вводят еще Цилиндрические функции второго рода (называемые также функциями Вебера):
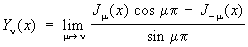
При помощи этих функций общее решение уравнения (1) может быть записано в виде
у = 1Jn(x) + 2n(x)
(как при целом, так и при нецелом n).
В приложениях встречается также Цилиндрические функции мнимого аргумента 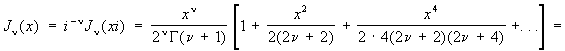 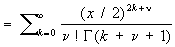
и
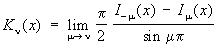
(функция Макдональда). Эти функции удовлетворяют уравнению
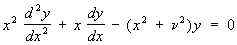
общее решение которого имеет вид
y = 1ln(x) + 2n(x)
(как при целом, так и нецелом n). Часто употребляются еще Цилиндрические функции третьего рода (или функции Ганкеля)
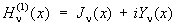
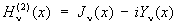 , ,
а также функции Томсона ber (х) и bei (x), определяемые соотношением
ber (x) + i bei (x) = 0(x 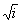 ). ).
Важную роль играют асимптотические выражения Цилиндрические функции для больших значений аргумента:
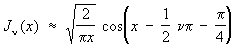 , ,
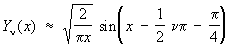 , ,
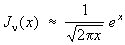 , ,
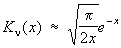 , ,
из которых, в частности, вытекает, что Цилиндрические функции Jn(x) и n(x) имеют бесконечное множество действительных нулей, расположенных так, что вдали от начала координат они как угодно близки к нулям функций, соответственно,
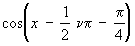 и и 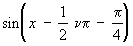
Цилиндрические функции изучены очень детально и для комплексных значений аргументов. Для вычислений существует большое число таблиц Цилиндрические функции
Лит.: Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М., 1969; Никифоров А. Ф., Уваров В. Б., Основы теории специальных функций, М., 1974; Ватсон Г. Н., Теория бесселевых функций, пер. с англ., ч. 1-2, М., 1949; Бейтмен Г., Эрдей А., Высшие трансцендентные функции, пер. с англ., 2 изд., т. 2, М., 1974. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 17:06:38
|

|

|
 |
|

|
 |
 |
 |
|