|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Хилла уравнение | Хилла уравнение (далее Х) мышечного сокращения, выражает изменение скорости сокращения мышцы в зависимости от ее нагрузки. Выведено английским физиологом А. В. Хиллом в 1938. Формула Х: ( + a)(v + b) = b (0 + а), где v — скорость сокращения мышцы при нагрузке , 0 — максимальное значение изометрической силы при тетаническом (см. Тетанус) раздражении всей мышцы, константы а и b — эмпирические величины. Константа а имеет размерность силы и равна около 4·105 дин/см2 поперечного сечения мышц различных видов, а константа b имеет размерность скорости (выражается в см/сек или l0/cek, где l0 — начальная длина мышцы) и для разных мышц различна.
В более общем виде эту закономерность выразили в 1953 английские ученые Б. С. Эббот и Д. Р. Уилки. Если сокращающаяся мышца имеет длину l в момент времени t, то скорость ее укорочения — dl/dt определяется по формуле: —dl/dt = (1 — ) b/( + а), где — сила, которую преодолевает мышца, 1 — максимальная сила мышц при той длине, при которой измеряется скорость ее укорочения, а и b — константы. Эта формула модифицирована Уилки в 1956, что позволило рассматривать скорость сокращения мышцы (—dx/dt) при любой заданной нагрузке во время тетанические сокращения всей мышцы: 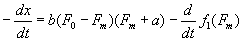 , где m — напряжение мышцы, пропорциональное тетаническому раздражению, f1(m) — характеристика зависимости напряжения от нагрузки для упругого элемента, соединенного последовательно, 0 — изометрическое (тетаническое) напряжение.
Скорость сокращения уменьшается при понижении температуры; температурный коэффициент Q10 равен около 2,5. Даже при отсутствии силы, противодействующей сокращению, мышца укорачивается с ограниченной скоростью: если = 0, то — (dl/dt) = 1b/a.
Х точно описывает сокращение мышц позвоночных н беспозвоночных, хотя еще не установлено соответствие констант уравнения сократительным, упругим и вязким элементам структуры мышцы. См. также Мышечное сокращение.
Лит.: Физиология мышечной деятельности, труда и спорта, Л., 1969 (Руководство по физиологии); Хилл А., Механика мышечного сокращения, пер. с англ., M., 1972; Abbott В. С., Wilkie D. R., The relation between velocity of shortening and the tension-length curve of skeletal muscle, "Journal of Physiology", 1953, v. 120; Wilkie D. R., The mechanical properties of muscle, "British Medical Bulletin", 1956, v. 12.
А. С. Батуев,
О. П. Таиров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.11.2024 18:34:58
|
|
|
|
|
|
|
|
|
|
|
