|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Хи-квадрат распределение | "Хи-квадрат" распределение (далее Х) с f степенями свободы, распределение вероятностей суммы квадратов
c2 = X12+...+Xf2,
независимых случайных величин X1,..., Xf, подчиняющихся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией. Функция "Х.-к." р. выражается интегралом
 , 
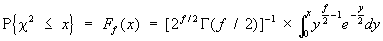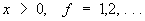
Первые три момента (математическое ожидание дисперсия и третий центральный момент) суммы c2 равны соответственно f, 2f, 8f. Сумма двух независимых случайных величин c12 и c22, с f1 и f2 степенями свободы подчиняется "Х.-к." р. с f1 + f2 степенями свободы.
Примерами "Х.-к." р. могут служить распределения квадратов случайных величин, подчиняющихся Рэлея распределению и Максвелла распределению. В терминах "Х.-к." р. с четным числом степеней свободы выражается Пуассона распределение:
 .
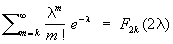Если количество слагаемых f суммы c2 неограниченно увеличивается, то согласно центральной предельной теореме распределение нормированного отношения 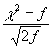 сходится к стандартному нормальному распределению:
 ,
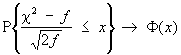где
 .
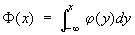
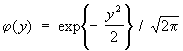Следствием этого факта является другое предельное соотношение, удобное для вычисления f (x) при больших значениях f:
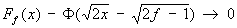
В математической статистике "Х.-к." р. используется для построения интервальных оценок и статистических критериев. Если 1,..., n — случайные величины, представляющие собой результаты независимых измерений неизвестной постоянной а, причем ошибки измерений i — а независимы, распределены одинаково нормально и
Е (i — a) = 0, Е (i — а)2 = s2,
то статистическая оценка неизвестной дисперсии s2 выражается формулой
 ,
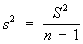где
 ,  .
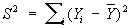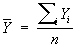Отношение 2/s2 подчиняется "Х.-к." р. с f = n — 1 степенями свободы. Пусть x1 и x2 — положительные числа, являющиеся решениями уравнений f (x1) = a/2 и f (x2) = 1 — a/2 (a — заданное число из интервала (0, 1/2)). В таком случае
Р {х1 < 2/s2 < x2) = Р {2/x2 < s2 < 2/x1} = 1—a.
Интервал (2/x1, 2/x2) называют доверительным интервалом для s2, соответствующим коэффициенту доверия 1 — a. Такой способ построения интервальной оценки для s2 часто применяется с целью проверки гипотезы, согласно которой s2 = s02(s02 — заданное число): если s02 принадлежит указанному доверительному интервалу, то делается заключение, что результаты измерений не противоречат гипотезе s2 = s02. Если же
s02 £ 2/x2 или s02 ³ 2/x1,
то нужно считать, что s2 > s02 или s2 < s02 соответственно. Такому критерию отвечает значимости уровень, равный a.
Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.
Л. Н. Большев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 14:17:39
|
|
|
|
|
|
|
|
|
|
|
